| Papers and Posters | Site Home Page |
New Approach to the Photochemical Kinetics in the Systems with Restricted Mobilities
Samuel Kh. Aranson*, Leonid A.Belyakov*, Sergei V.Zelentsov**, and Vadim D.Lebedev
*** Applied Mathematics and Kibernetics Institute at the Nizhnii Novgorod State University,
** Chemical Department, Nizhnii Novgorod State University,
Gagarin Ave., 23. Nizhnii Novgorod, 603600, Russia.
E-mail: zelen@ichem.unn.runnet.ru
Summary.
It was developed the PDE systems describing the photochemical kinetics with usage of the differential version of the Buger-Lambert-Berr law. New method of exact solution of the PDE systems was proposed. It is shown that if one takes u.v. irradiation intensity and current time as independent variables then initial systems splits into the set of ODE with the boundary conditions imposed.
The results obtained can be used in kinetical studies of photochemical reactions in media of low reagents mobilities.
1. Introduction.
Modern photochemistry met a demand to study the reactions in media with restricted mobilities of reagents. In the case of the reactions there is non-equivalence of molecules contained in a sample in respect to intensity of u.v. light irradiating them. From the mathematical point of view that means that the differential version of the Buger-Lambert-Berr law but not the integrated one is to be used [1-4].
A sample irradiated with u.v. radiation may be treated as an infinite sum of "elementary photochemical reactors". If transfer of matter is limited in the "reactors" then u.v. radiation intensity acting upon the molecules in the reactor should be considered to be constant and the photochemical reaction rate constant should be proportional to the intensity and the quantum yield of the reaction. Lowering of intensitynE passed through the layer is proportional to E at the upper boundary, to layer thickness, D x, and a sum of products of extinction coefficient and concentration of every substance involved in the photochemical reaction. When D x ® 0 then there has place the differential version of the Buger-Lambert-Berr law, i.e.
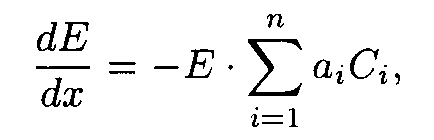
where n is a number of reagents involved in the reaction, Ci is concentration of the i-th substance having extinction coefficient ai in the layer ("reactor") under consideration.
Similar models were formulated in papers [1-4]. However there was no an analytical presentation of exact or approximate solutions of them even in the simplest cases. The desire of solutions of the kinetics problems in the analytical forms is dictated by complexity of the results of the photochemical kinetical researches especially in the media with low mobilities of the reagents.
It should be noted that mathematical models of photochemical kinetics contain the partial differential equations (PDE). Numerical solutions of the PDE sets are hard to process and the results of such calculations are not easy to rationalize, they are not convenient to look through and use.
The aim of the paper presented is to obtain analytical expressions that describe photochemical kinetics and explicitly take into account changing of u.v. light intensity irradiating reacting molecules in the entire reaction system.
2. The mathematical models describing kinetics of the simplest photochemical reactions.
The PDE systems describing the kinetics of the simplest reaction may be written down as following.
(1) The A
A + hn ® B B A A + hn ® B B B B A A A + hn ® B B reaction.The reaction consists of the only photochemical reaction A
® B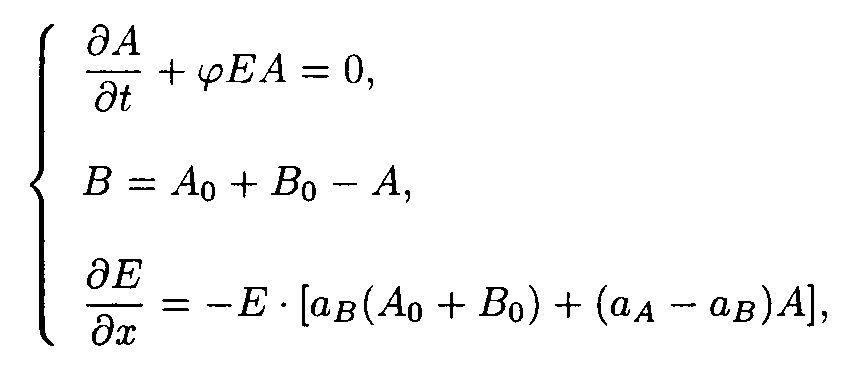
The boundary and starting conditions such as A(x,0) = Ao, B(x,0) = Bo, and E(0,t) = Eo are to be imposed.
(2) The A
A + hn ® B B A A + hn ® B B A A + hn ® B B B B B B and B B B B ® A A reactions.The reaction system consists of two processes, the A
® B reaction occurring under u.v. irradiation and the B ® A reaction being initiated thermally.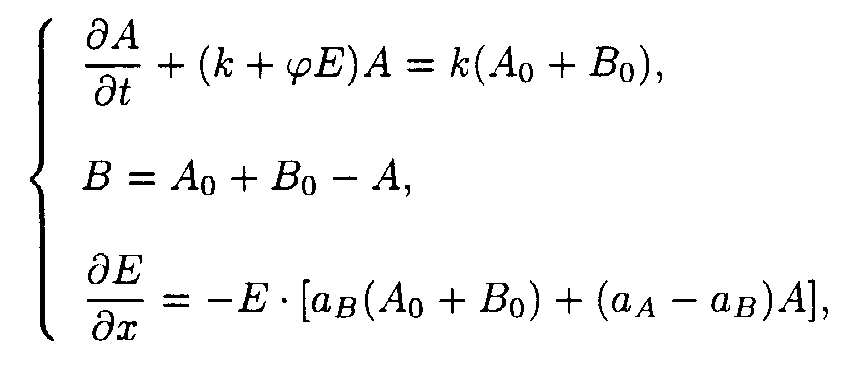
The boundary and starting conditions such as A(x,0) = Ao, B(x,0) = Bo, and E(0,t) = Eo are to be imposed.
(3) The A
+ hn ® B and B ® C reactions.The reaction system consists of two processes, the A ® B reaction occurring under u.v. irradiation and the B ® C reaction being initiated thermally.
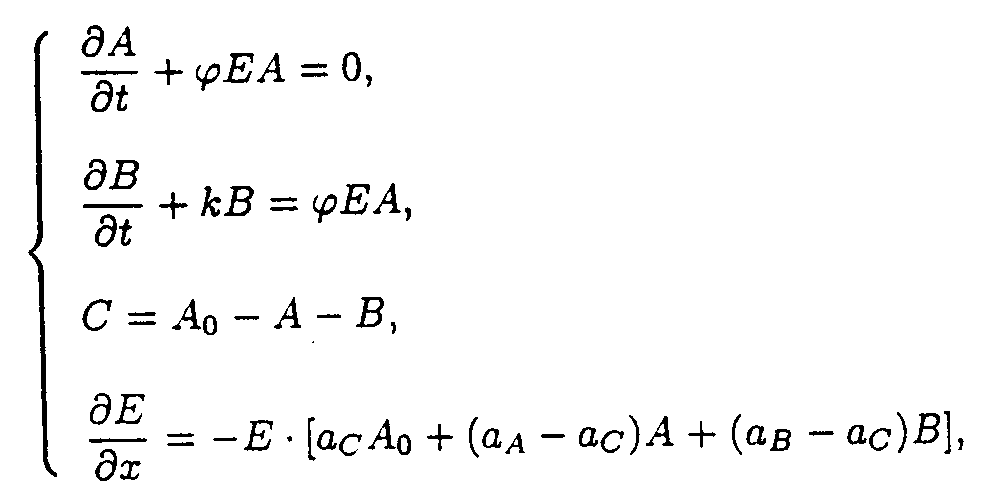
The boundary and starting conditions such as A(x,0) = Ao, B(x,0) = Bo, and E(0,t) = Eo are to be imposed.
(4) The A
A + hn ® B B A A + hn ® B B B B and B B B B + hn ® C C reactions.The reaction system consists of two processes, the both reactions being photochemical.
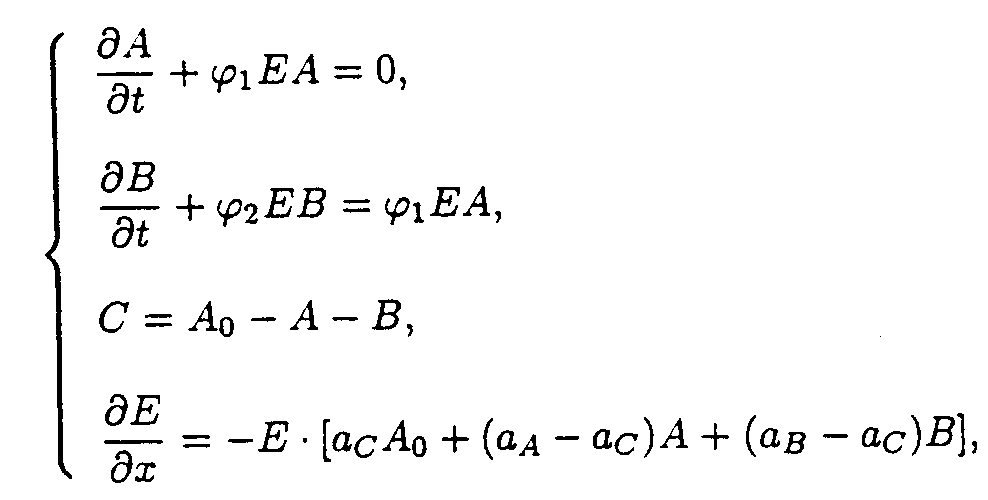
The boundary and starting conditions such as A(x,0)=Ao, B(x,0)=Bo, and E(0,t)=Eo are to be imposed.
We adopted the following designations: A=A(x,t), B=B(x,t), and C=C(x,t) are current concentrations of substances A, B, and C, [M· m-3]; E=E(x,t) is u.v. light intensity at x distance from the irradiated surface of the sample, [W· m-2]; Eo is u.v. intensity at the surface of the irradiated sample, [W· m-2]; j , j 1, and j 2 are effective rate constant of the corresponding photochemical reactions, [j-1· m2]; aA, aB, and aC are absorbencies of substances A, B, and C, [M-1· m2]; k is rate constant of thermally initiated reaction having first order, [s-1]; x is distance from the layer under consideration to irradiated surface of the sample, [m]; h is thickness of the sample, [m]; t is current time, [s].
It is possible to generalize the systems to do their analysis more simple. Let us write the system of the model 1 (including reactions 1 and 2) as
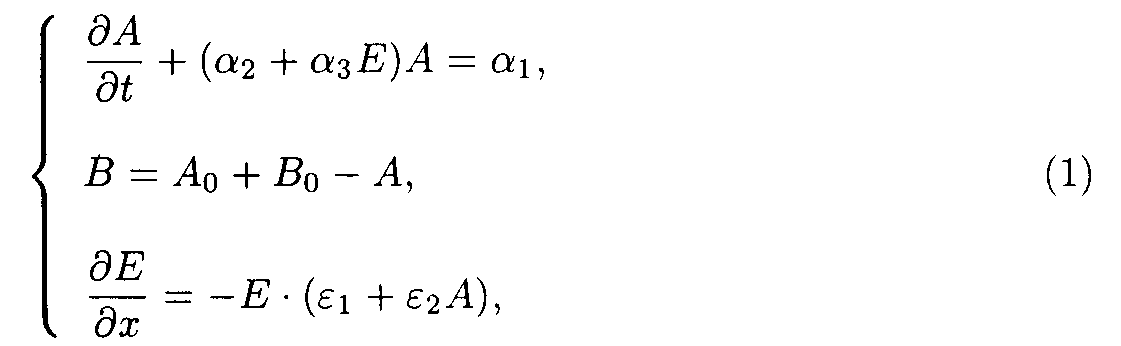
The boundary and starting conditions such as A(x,0)=Ao, B(x,0)=Bo, and E(0,t)=Eo are to be imposed. The parameters of model 1 are shown in the table 1.
Table 1. Parameters of the model 1.
No. of reaction system |
|
a 2 |
a 3 |
e 1 |
e 2 |
||||
|
k(Ao+Bo) |
0 k |
j j |
aB(Ao+Bo) aB(Ao+Bo) |
aA-aB aA-aB |
The system of model 2 (including reactions 3 and 4) may be written as
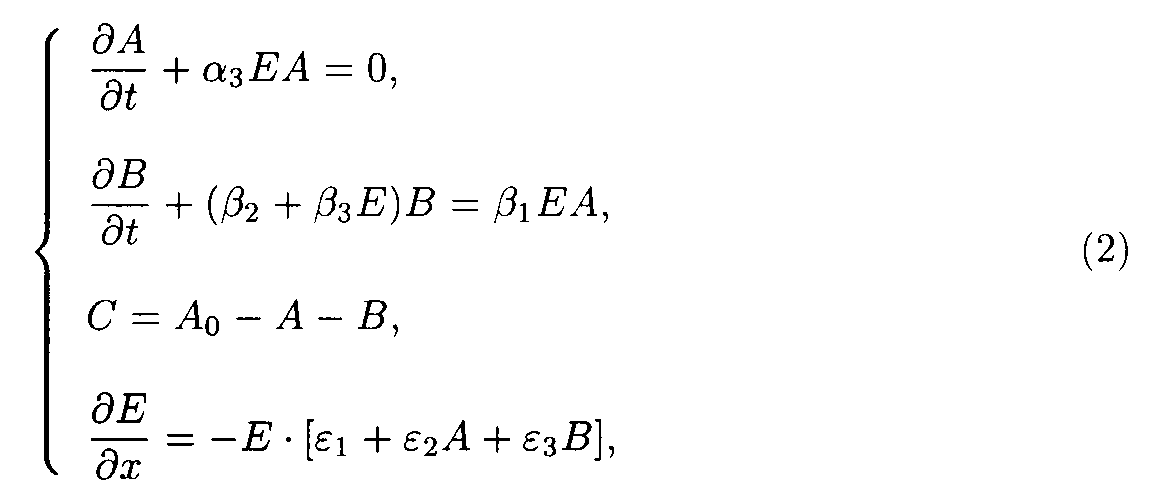
The boundary and starting conditions such as A(x,0)=Ao, B(x,0)=Bo, and E(0,t)=Eo are to be imposed. The parameters of model 2 are shown in the table 2.
Table 2. Parameters of the model 2.
No. of reaction system |
a 3 |
b 1 |
b 2 |
b 3 |
e 1 |
e 2 |
e 3 |
||
|
j j 1 |
j j 1 |
k 0 |
0 j 2 |
aCAo aCAo |
aA-aC aA-aC |
aB-aC aB-aC |
3. Solution of the system describing of the model 1.
So as ¶ E/¶ x ¹ 0 for all x ³ 0, and t ³ 0, one may take u.v. irradiation intensity and current time as independent variables. Then the initial system (1) splits into the set of ordinary differential equations (ODE) with separated boundary conditions imposed.
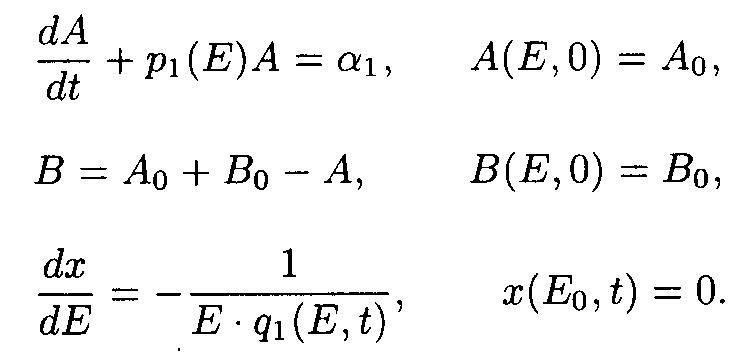
Here p1(E)=a 2+ a 3E, q1(E,t)=e 1+ e 2A(E,t).
Exact solutions for the set of ODE may be written as following:
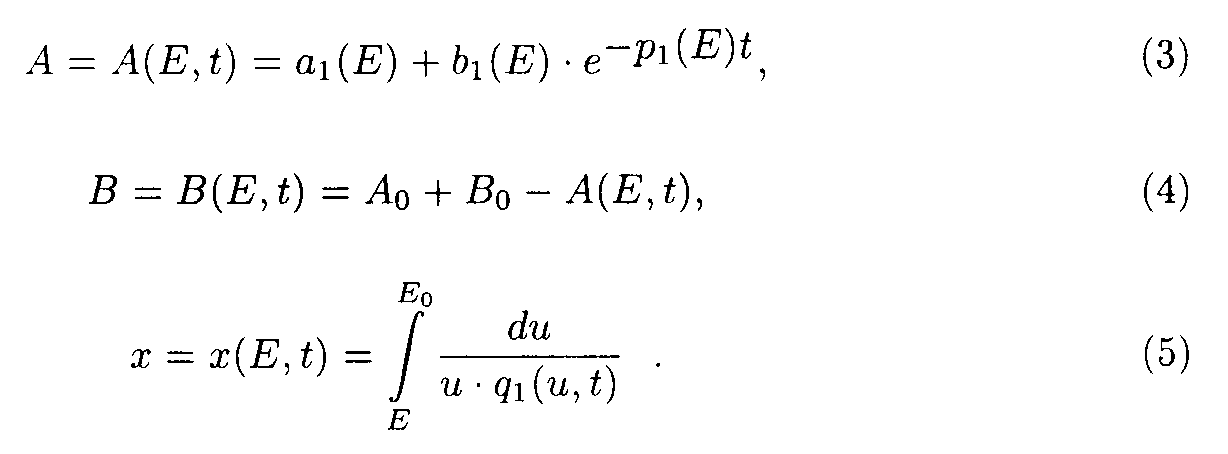
Here
a1(E) = a 1/p1(E); b1(E) = Ao- a1(E).
Exact solution such as eq.(5) contains special functions therefore the procedure of deriving approximate solutions desires to be given to do a practical use more convenient.
Taking into account only the first term of Taylor's expansion of q1(E,t).
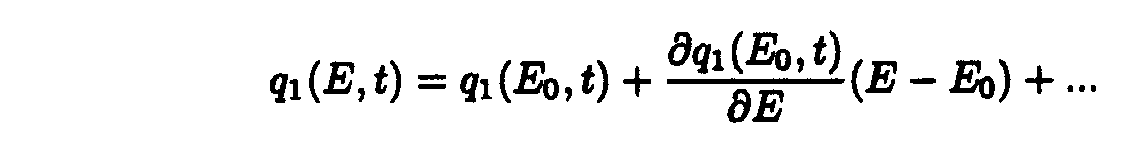
one may obtain
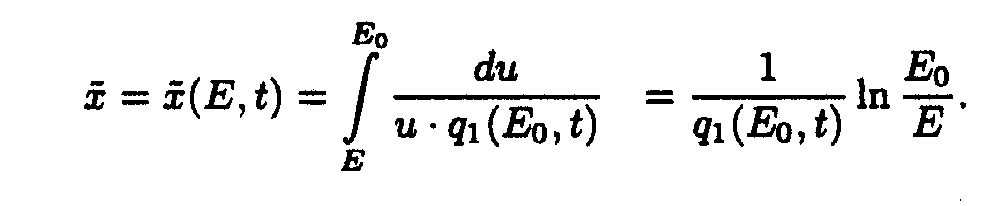
It is easy to show [5] that if
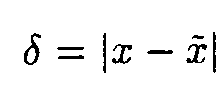
then
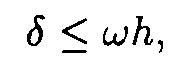
where
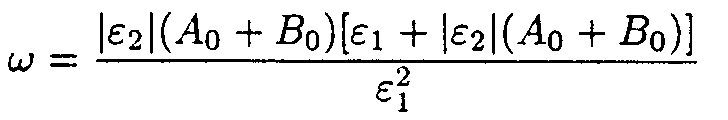
4. Solution of the system describing the model 2.
As in the case of the first system one may take u.v. irradiation intensity and current time as independent variables. Then the initial system (2) splits into the set of ODE with separated boundary conditions imposed.
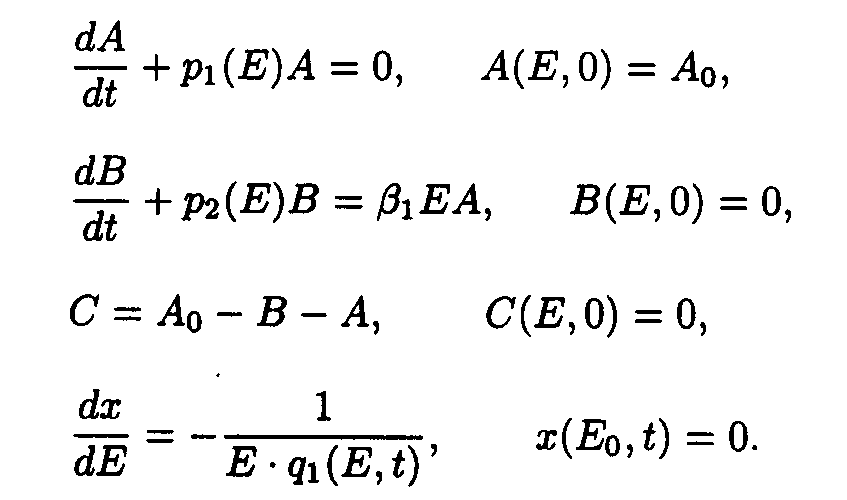
Here we adopted the following designations:
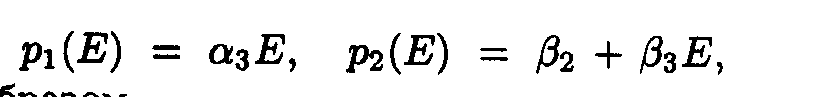
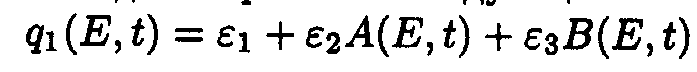
Exact solutions for the set of ODE may be written as following:
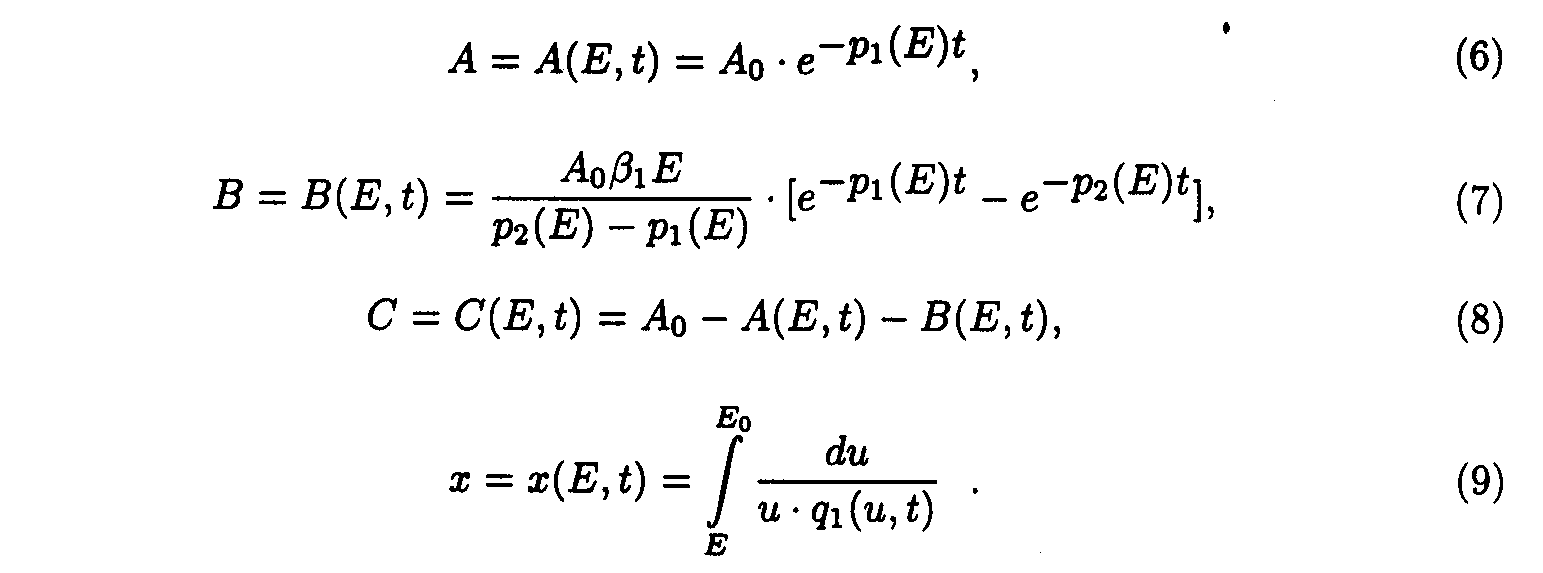
Exact solutions such as eq.(9) contains special functions therefore the procedure of deriving approximate solutions desires to be given to do a practical use more convenient.
Taking into account only the first term of Taylor's expansion of q1(E,t), one may write down
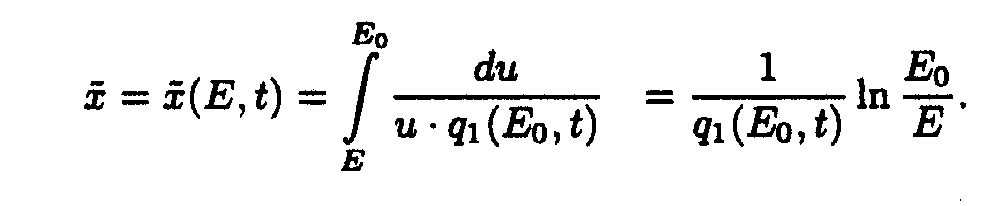
It is easy to show [5] that if
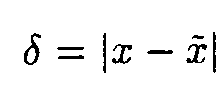
then
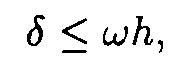
where
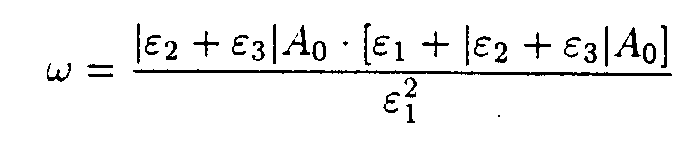
5. Discussion of the results.
We were able to receive exact solutions of the kinetics equations in 4 simple cases. The method used may be successfully used not only in the cases but for other systems with limited mobilities of reagents. So it has methodological usefulness. Although the expression for u.v. light intensity at distance x from the surface having been irradiated is given in implicit form and its direct usage meets some difficulties it may be use to derive the family of approximations having different precision.
To make usage of our results more convenient and easy we derived explicit expressions in the (E,t) coordinates system and in more ordinary for photochemists the (x,t) coordinate system.
Reaction system (1).
In the (E,t) coordinate system
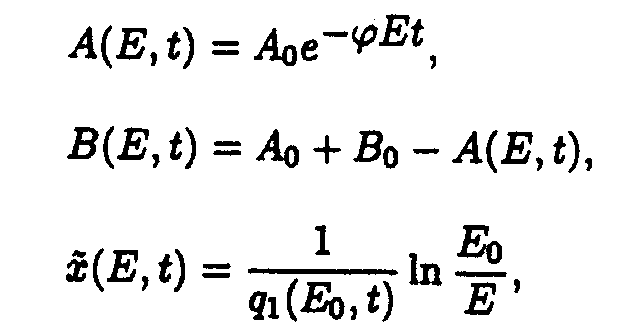
where
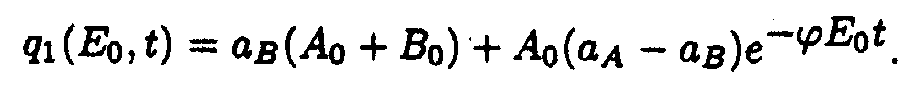
In the (x,t) coordinates system
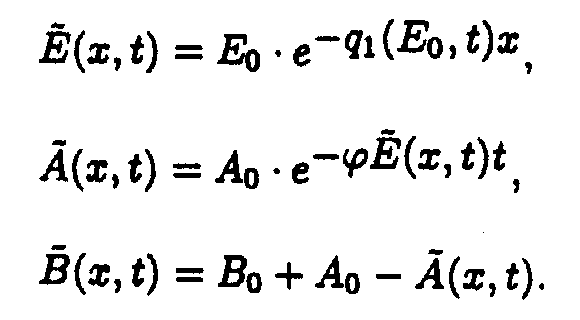
Reaction system 2.
In the (E,t) coordinate system
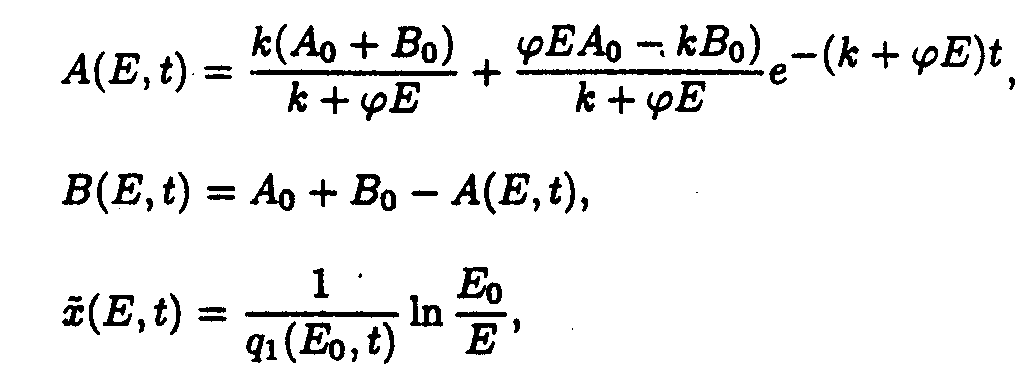
where
![]()
In the (x,t) coordinate system
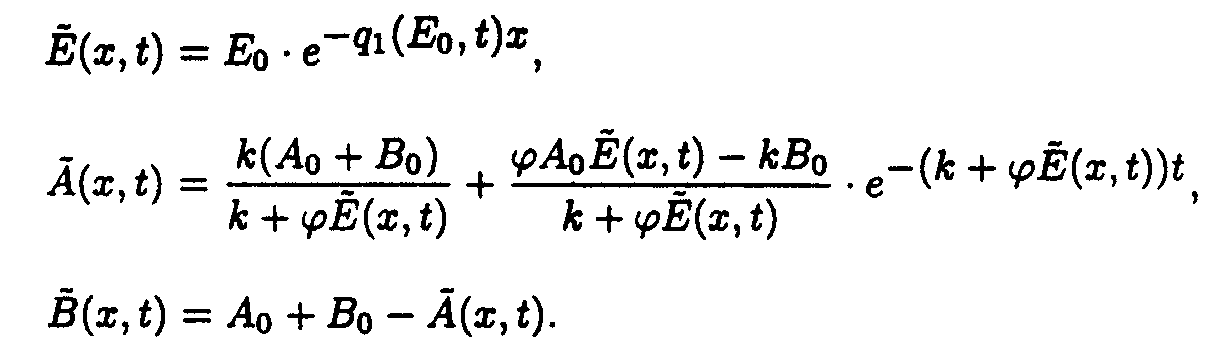
Reaction system 3.
In the (E,t) coordinates system
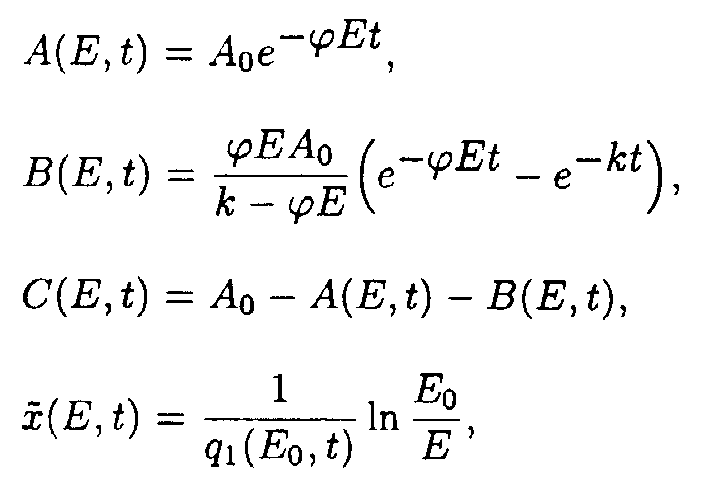
where
![]()
In the (x,t) coordinate system
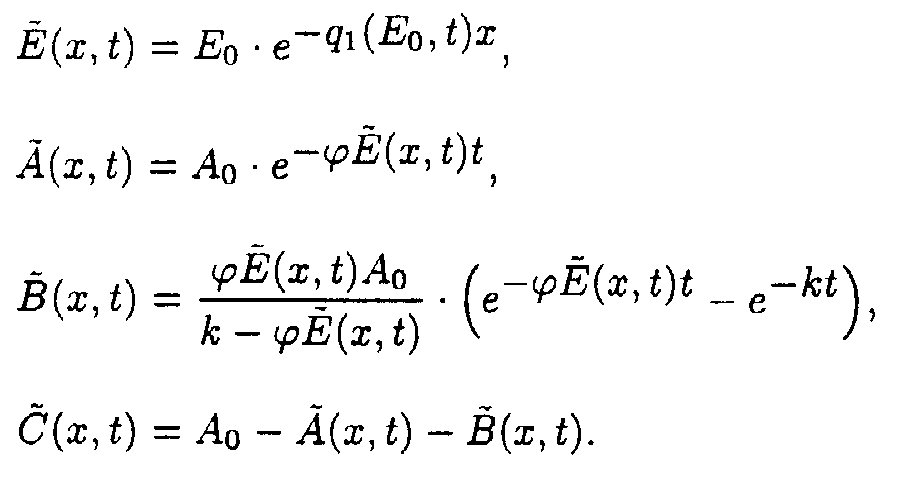
Reaction system 4.
In the (E,t) coordinate system
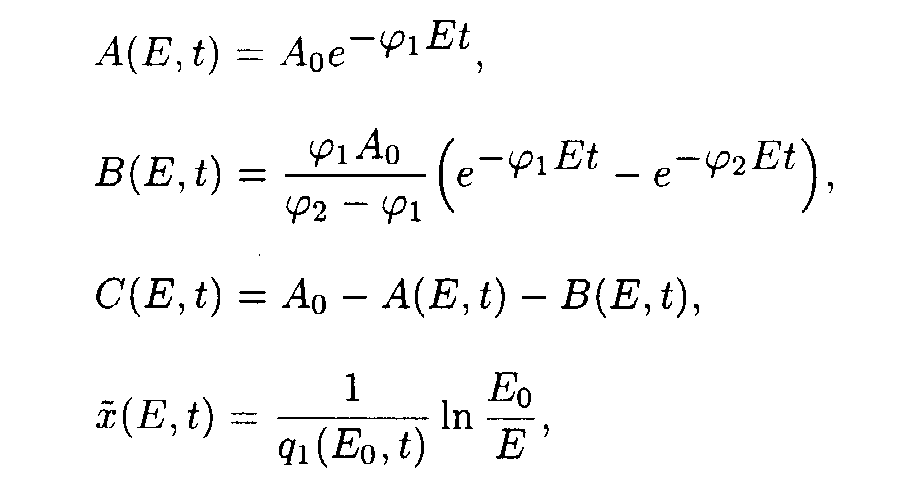
where
![]()
In the (x,t) coordinate system:
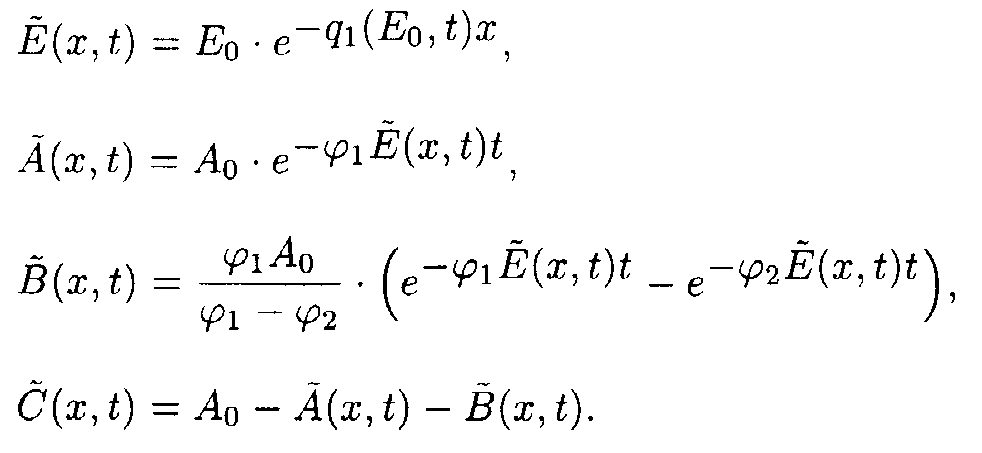
It should be noted once more that in the (E,t)- coordinate system it is possible to use numerical methods to calculate integrals (5) and (9) and evaluate function x(E,t) with every tolerance desired.
Thus we developed the method that may be used not only in the case of the systems described but for more general class of photochemical kinetics problems. The only condition limiting its usage is absence of diffusion in the reaction systems.
Acknowledgment. We thanks the RFBR (grants No.99-01-00230, 98-01-00795), and INTAS (grant 97-1843) and Interdepartmental Scientifical and Technical Program "Chemistry" ("Photochemistry" division) (Russian Gov.Com.) for financial support of the research.
REFERENCES
1. Mauser N.// Z.Naturforsch. 1979. B.234. No.12. S.1264
2. Vorob'ev A.Kh., Gurman V.S.// High Energy Chem. 1985. V.19. No.2. P.148.
3. Yanin A.M., Treushnikov V.M., Karyakina L.N., and Oleinik A.V.// High Energy Chem. 1988. V.22. No.2. P.142.
4. Treushnikov V.M., Tscherednik V.I., and Oleinik A.V.// J.Sci.and Appl. Photogr. and Cinematogr. (Russ.) 1987. V.32. No.4. P.308
5. Aranson S.Kh., Belyakov L.A., Zelentsov S.V., Oleinik A.V. and Lebedev V.D.// Proc. of Nizhnii Novgorod State Univ. Ser."Math.Simul. and Optimal Control". 1999. P.46-53.