| Papers and Posters | Site Home Page |
A Semiempirical Study for the Ground and Excited States
of Free-Base and Zinc Porphyrin-Fullerene Dyads

Andreas B.J. Parusel
NASA Ames Research Center, MS 239-4, Moffett Field, CA 94035, USA;
fax: +1-650-604 1088; email: parusel@camelot.arc.nasa.gov

![]()
Abstract:
The ground and excited states of a covalently linked porphyrin-fullerene dyad in both its free-base and zinc form (D. Kuciauskas et al., J. Phys. Chem. 1996, 100, 15926) are investigated by semiempirical methods. The excited state properties are discussed with respect to the character of the molecular orbitals. All frontier MO´s are mainly localized on either the donor or the acceptor subunit. Thus, the absorption spectra of both systems are best described as the sum of the spectra of the single components. The experimental observed spectra are well reproduced by the theoretical computations. An electron transfer (ET) is found in experiment in polar but not in apolar solvents. This observation is explained by taking into account solvent effects into the calculations. The in vacuo tenth excited state is of charge separated (CS) character with an electron being transferred from the porphyrin donor to the fullerene acceptor subunit. This ET state is stabilized significantly in energy by the solvent due to its large formal dipole moment. The stabilization energy for apolar benzene is not sufficient to lower this state down to the S1. Thus, no electron transfer is observed in agreement with experiment. In polar environment like acetonitrile, the charge separated state becomes the S1 and an electron transfer takes place, as observed in experiment. The flexible single bond connecting both the donor and acceptor subunit allows free rotation about ±30° about the optimized ground state conformation. For the charge separated state this optimized geometry has a maximum dipole moment. The geometry of the charge separated state thus not changes relative to the ground state conformation. The electron donating properties of porphyrin are enhanced in the zinc derivative due to a reduced porphyrin HOMO-LUMO energy gap. This yields in a lower energy for the charge separated state compared to the free base dyad.
![]()
1. Introduction
Electron transfer (ET) from a donor to an acceptor unit belongs to the most fundamental processes in both natural and artificial systems. Since the early beginnings of life this process of charge separation (CS) has been used by nature to convert light energy into chemically storable energy. Innumerable attempts have been made to get a closer insight into the understanding of photoinduced electron transfer and charge transfer (CT) processes in natural systems. We are still far away from understanding these mechanisms for large and complex molecules, thus researches on more simple molecular systems is of major importance. Such model investigations are necessary for a better understanding of the photosynthesis processes [1,2], which is of interest for the manufacturing of energy producing machines on a nanometer scale [3].
A longliving charge separated state is the primary requirement for a system modeling the photosynthetic reaction center. Several molecular dyads of the general donor-acceptor type have been investigated with respect to this problem (for a review see e.g. ref. [4]). Porphyrins play a major role as the electron donating part of the dyad due to their excellent electron donating properties and their common presence in nature. Both free-base and metallated porphyrins have been investigated in detail, the latter having got even improved electron-donating properties. Fullerenes gained increasing interest in chemistry since their first synthesis. Their strong electron accepting properties make them ideal candidates as acceptor part of molecular D-A dyads [5-11].
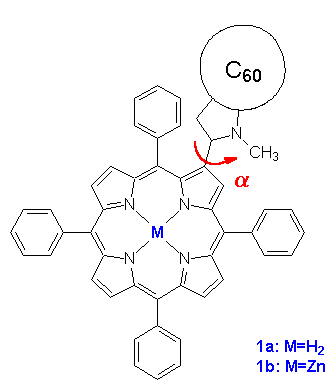
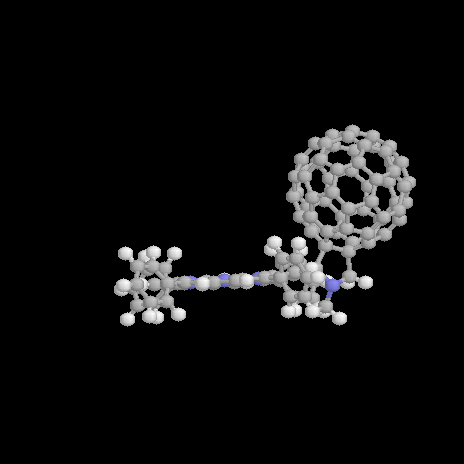
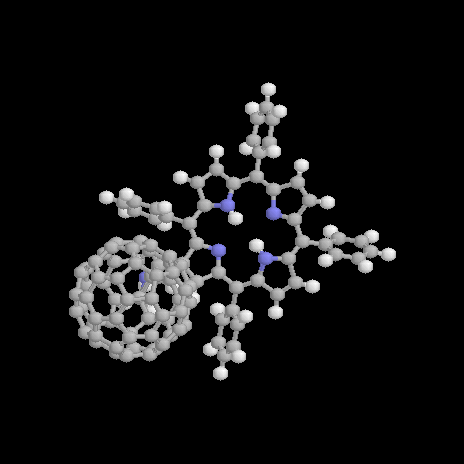
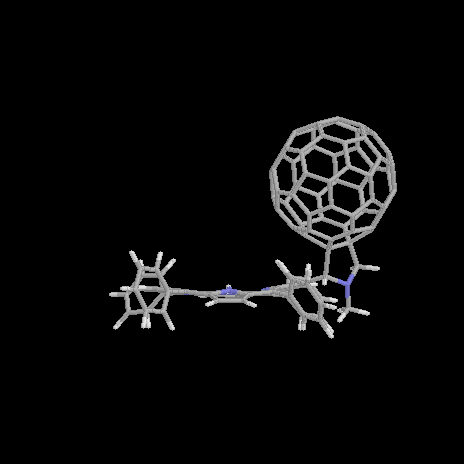
Figure 1. Structure of the free base (1a) and zinc (1b) porphyrin-fullerene dyad; definition of the rotation angle a.
Recently, an excellent example of a covalently linked porphyrin-fullerene dyad has been presented and investigated experimentally [8]. For the structure of both the free-base and zinc dyad 1a and 1b see Figure 1. An efficient energy and photoinduced electron transfer is observed experimentally in both systems. The lifetime of the charge-separated states are detected to be as long as 290 ps for 1a and of 50 ps in the zinc derivative 1b. [8] This makes these systems ideal candidates as components of light-harvesting systems and photomolecular devices. An electron transfer takes place in benzonitrile and comparable polar solvents but is not observed in apolar solvents as toluene [8]. The first excited singlet state of the porphyrin is deactivated by singlet-singlet energy transfer to the fullerene. An almost totally quenching of the porphyrin emission accounts for this energy transfer deactivation pathway and is confirmed by corrected fluorescence excitation spectrum for fullerene emission [8] A similar behavior of electron and energy transfer is found also in a dyad separated by an extended bridged C60 porphyrin dyad [9]. Thus, this behavior is typical for a porphyrin fullerene dyad in general and not determined exclusively by the length and character of the spacer.
In the first part of this study, an analysis of the ground state of system 1a is presented. In the second part, the character and energies of the frontier molecular orbitals for both the free base 1a and metallated system 1b are investigated. Further, the excited states are characterized and the semiempirical results are compared to experimental data.
![]()
2. Computational methods
Quantum mechanical calculations of the ground and excited states are carried out using version 7.0 of the program package VAMP [12] applying the AM1 Hamiltonian [13]. Ground state geometry optimizations are carried out starting from different geometries. A subsequent frequency analysis is carried out to exclude localizing a local minimum. No electron correlation is taken into account for the ground state optimizations. A detailed molecular orbital analysis as described later (cf. 3.1) determines the active space for computation of excited state properties. They are obtained from a configuration interaction scheme including all single and pairwise double excitations (AM1/PECI) [14] within an active space of 20 orbitals, i.e. including all molecular orbitals in-between HOMO-9 and LUMO+9. This yields 301 configurations. The rotation angle a as defined in Figure 1 describes the relative orientation of porphyrin and fullerene subunit. A reaction coordinate with varying angles a is obtained by keeping fixed the rotation angle a with all other degrees of freedom optimized independently.
Solvent effects are estimated in dependence on the cavity radius for solvents of different polarity. Solvation energies for the excited states are calculated by two different approaches considering solvent influences on absorption spectra on the hand and state energies on the other hand. In the first case, reorientation of the solvent molecules is disregarded. The solvent shifts of electronic absorption transitions are calculated according to the Lippert theory [15] by:
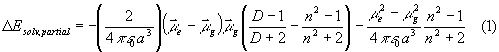
where a is the cavity radius (for determination of a, see 3.3), mg is the ground state dipole moment, me is the excited state dipole moment, e 0 is the universal dielectric constant, D is the dielectric permittivity, and n is the refractive index.
Allowing full reorientation of the solvent molecules according to the charge distribution in the relaxed excited state yields the total solvation energy according to Lippert [15]:
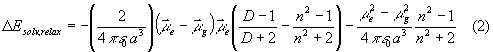
The total energies of excited states in a solvent are obtained by adding the respective solvation energy DE to the gas phase transition energies. In order to allow comparison with experiment, the calculations are carried out for acetonitrile as a polar aprotic solvent with e = 35.94 and n = 1.342 and benzene as a apolar solvent with e = 2.27 and n = 1.498. It is important to notice that small changes in the cavity radii cause large shifts in the computed stabilization energy; in particular, the charge separated state is sensitive to this parameter due to its huge formal dipole moment. Thus, the results of the solvent computations are used to present general effects and reversal of excited states orderings, and not to predict absolute numbers.
![]()
3. Results and Discussion
3.1 Electronic Ground State
|
|
|
Figure 2. Optimized structure of 1a in side (left), top (middle), and front (right) view. |
||
The geometry optimization of 1a results in a geometry presented in Figure 2. The total energy is computed to be 1328.7 kcal/mol with a dipole moment m=4.7 D. The optimized dihedral angles of the four phenyl groups attached to the porphyrin are 62°. It has been shown elsewhere [16] that the orientation of these groups only has only got a neglectigable effect on the electronic properties of a molecular dyad. There orientations are thus not further considered throughout the text. The pyrrolidine nitrogen shows a typical sp3 hybridized pyramidalization of 25°. The orientation of the C60 unit relative to the porphyrin is determined by the rotation angle a (for a definition see Figure 1) about the single bond connecting the porphyrin and the pyrrolidine ring attached to the fullerene. A center-to-center distance d between the fullerene to the porphyrin of d=9.9Å is computed for 1a in its optimized ground state. The reaction coordinate for rotation a from a=30° to a=120° about the single bond is shown in Figure 3.
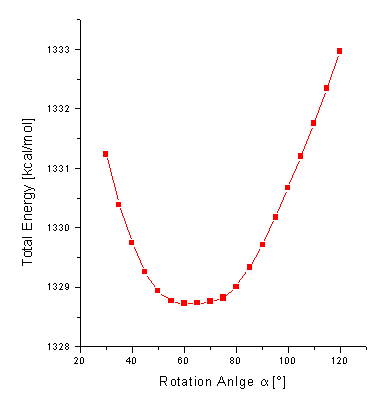
Figure 3. Total Energy in kcal/mol of the dyad 1a as a function of the rotation angle a in [°].
A free rotation a at room temperature is observed within the region from a=45° to a=85°, with the total energy less than 0.5 kcal/mol higher than that of the optimized geometry. Three exemplary conformers with a=62° (minimum), a=30°, and a=100° are presented in Figure 4. The center-to-center distance is reduced to 9.4Å for a=30° and increased to 10.6Å for a=100°. The dependency of the total energy on the rotation angle a is much stronger for smaller than for larger angles a. For a=30° (i.e. Da=-30°) DHf=+2.5 kcal/mol, whereas only DHf=+1.0 kcal/mol are computed for rotation to a=90° (i.e. Da=+30°). The deeper ascent in energy goes along with a decrease in the center-to-center distance d (i.e. smaller rotation angle a) caused by a larger sterical hindrance between the porphyrin and fullerene subunits. This can be seen in the more twisted geometry of the porphyrin, shown in Figure 4 (left).
|
|
|
Figure 4. Optimized structure of 1a with a=30° (left), a=62° (middle), and a=100° (right). |
||
The ground state geometry of the zinc metallated dyad 1b deviates only marginally from that of 1a. This corresponds to the results for a comparable free-base and metallated porphyrin-flavin dyad [16]. The center-to-center distance is 9.9Å as for 1a. The total energy Hf is computed to be 1358.4 kcal/mol, the dipole moment is slightly larger (m=5.9 D). The zinc atom is located in the porphyrin plane with a distance of 2.06Å to the nitrogen atoms.
3.2 Frontier Molecular Orbitals
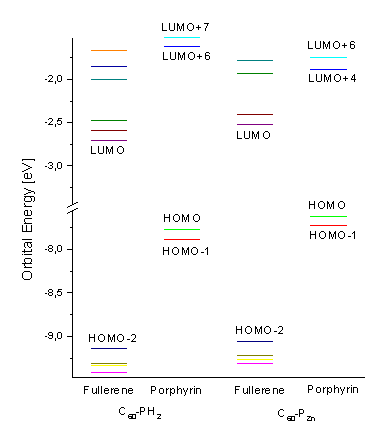
Figure 5. Orbital energy (eV) of the frontier orbitals of the free-base (1a, left) and zinc (1b, right) porphyrin-fullerene dyads.
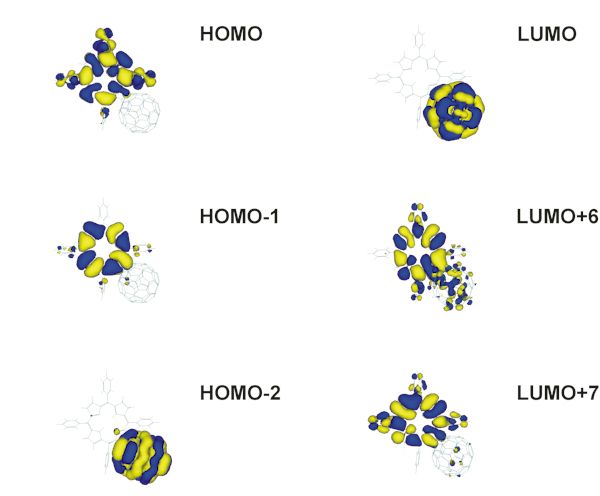
Figure 6. Visualization of the decisive occupied (left) and unoccupied (right) MO’s of the dyad 1a.
The energies of the frontier orbitals of the free base (1a) and metallated (1b) dyad are presented in Figure 5. All decisive orbitals of the dyads are localized on one of the single components, i.e. either the porphyrin or the fullerene subunit. The four porphyrin and two fullerene frontier orbitals are visualized in Figure 6. Only the LUMO+6 partially expands its virtual orbital character into the fullerene. The HOMO-1, HOMO, LUMO+6, and LUMO+7 of 1a are of porphyrin character and correspond to the four frontier orbitals according to the Gouterman four-orbital model for porphin [17]. The energy of the porphyrin HOMO is significantly higher than the energy of the fullerene HOMO (HOMO-2), thus assigning this subunit as the electron donor of the dyad. Also the fullerene LUMO is lower in energy compared to the porphyrin LUMO (LUMO+6) by approximately 1 eV, assigning this unit as the electron acceptor. This is in agreement with experimental results [8].
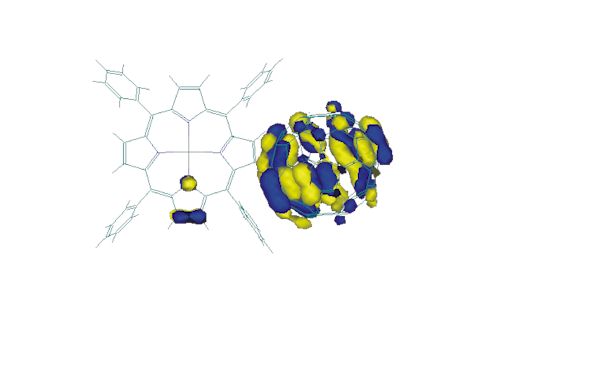
Figure 7. Visualization of the HOMO-2 of the zinc dyad 1b
The characters of the two occupied porphyrin orbitals HOMO and HOMO-1 remain almost unchanged when substituting the two central hydrogen atoms in 1a by the zinc atom in 1b. Its orbital energies are slightly higher. In contrast, the zinc atom significantly stabilizes the two unoccupied porphyrin frontier orbitals, the LUMO+6 and LUMO+7 for 1a. Thus, these two orbitals become the LUMO+4 and LUMO+6 for 1b. This stabilization along with the small destabilization of the porphyrin HOMO´s causes a decrease in energy gap between the two occupied and unoccupied porphyrin frontier orbitals. The HOMO-2 represents the highest occupied molecular orbital of the dyad 1b, which is localized at the C60 acceptor subunit. Additional p character at one of the pyrrole units in the porphyrin is calculated for this MO (see Figure 7). The HOMO-3, HOMO-4, LUMO and next higher unoccupied MO´s are purely of fullerene character for both 1a and 1b. A minimum active space of 16 orbitals (i.e. from the HOMO-7 up to the LUMO+7) has to be included in the calculations of the excited state properties, to consider the two unoccupied MO´s of porphyrin character. To allow more flexibility, an active space of twenty molecular orbitals is chosen, i.e. from HOMO-9 to LUMO+9.
3.3 Electronic Excitations
Table I.
Excitation Energies (DE in eV), Dipole Moments (m in D), Oscillator Strengths f, and Characterization of the First Excited Singlet States for the Free-Base Dyad 1a. "Character" Describes the Main Configurations of the Excitations.
D E |
m |
f |
Character |
||
S1 |
P*-C60 |
2.34 |
5.2 |
0.001 |
HOMOà LUMO+7 HOMO-1à LUMO+6 |
S2 |
P*-C60 |
3.00 |
6.7 |
0.003 |
HOMOà LUMO+6 HOMO-1à LUMO+7 |
S3 |
P-C60* |
3.30 |
6.0 |
0.000 |
HOMO-2à LUMO+1 |
S4 |
P-C60* |
3.31 |
7.5 |
0.049 |
HOMO-2à LUMO |
S5 |
P-C60* |
3.39 |
5.0 |
0.001 |
HOMO-4à LUMO |
S6 |
P-C60* |
3.43 |
5.2 |
0.000 |
HOMO-3à LUMO |
S8 |
P*-C60 |
3.59 |
6.0 |
0.924 |
HOMOà LUMO+7 HOMOà LUMO+6 HOMO-1à LUMO+6 HOMO-1à LUMO+7 |
S10 |
P+-C60- |
3.64 |
42.7 |
0.009 |
HOMOà LUMO HOMO-1à LUMO |
S14 |
P*-C60 |
3.71 |
5.6 |
1.042 |
HOMO-1à LUMO+6 HOMOà LUMO+6 HOMOà LUMO+7 HOMO-1à LUMO+7 |
The properties of the excited singlet states of free base dyad 1a are summarized in Table I. The first and second excited state are of porphyrin character. They result from the combination of exciting an electron from one of the nearly degenerate orbitals HOMO-1 and HOMO into either theLUMO+6 or LUMO+7. The S1 and S2 states have excitation energies of 2.34 eV and 3.00 eV, a small oscillator strength of less than 0.01 and a dipole moment of 5.2 D, and 6.6 D. These excitations can be assigned to the two Q bands of the experimental absorption spectrum at an energy of 1.90 eV and 2.23 eV, respectively [8]. The excitation energies of the next four states are calculated to lie between 3.3 eV and 3.4 eV, with a small oscillator strength. They correspond to the first excitations within the fullerene unit. According to Kuciauskas et al. and Gust [8,18], the fullerene first excited state is located at 1.74 eV. It is not found by analyzing the semiempirical results. This experimental low energy P-C60* state is in agreement with the absorption spectra of free C60 isolated in Argon matrices [19], where two forbidden singlet states of 1T2u symmetry in the region of 3.1 eV and 1T1g symmetry at about 2.0 eV are postulated. Also the time dependent density functional theory calculations (TDDFT) of Bauernschmitt et al. [20] locate the first and second excited singlet state in free C60 at 2.82 eV and 3.51 eV, respectively. Thus the forbidden low energy excited states are also not computed. The optically allowed excited states of the fullerene part of the spectrum are found experimentally in the region above 3.0 eV [8] (see also [9]), properly calculated by the semiempirical AM1 Hamiltonian (> 3.3 eV). It is therefore not possible to reproduce the energy transfer step from the first excited porphyrin state (exp: 1.90 eV, theory: 2.34 eV) to the first excited fullerene state (exp: 1.74 eV, theory: 3.30eV) as observed in experiment. The energies of the eighth and fourteenth excited state with a large oscillator strength are computed to be 3.50 eV (m=6.0 D, f=0.924) and 3.71 eV (m=5.6 D, f=1.042) and are assigned to the experimental Soret band. The two states are characterized by a mixed excitation within the four porphyrin frontier orbitals. The energy is too high by ca. 0.6 eV in comparison to experiment, where the Soret band is observed at about 2.9 eV [8].
Table II. Excitation Energies DECS [eV] and Stabilization Energies DEsolv,relax [eV] for the Charge Separated State in Gasphase, Benzene, and Acetonitrile for Different Rotation Angles a [°]. The Corresponding center-to-center distances d [Å], cavity radii a [Å], and Dipole Moments m [D] are given as well.
D ECS |
D Esolv,relax |
D ECS |
D Esolv,relax |
D ECS |
D Esolv,relax |
|
Gasphase |
3.53 |
3.64 |
3.67 |
|||
Benzene |
3.00 |
0.53 |
3.02 |
0.62 |
3.23 |
0.44 |
Acetonitrile |
1.65 |
1.88 |
1.60 |
2.04 |
2.28 |
1.39 |
a |
30 |
62 |
100 |
|||
d |
9.4 |
9.9 |
10.6 |
|||
a |
7.1 |
7.5 |
8.0 |
|||
m |
36.6 |
42.7 |
39.7 |
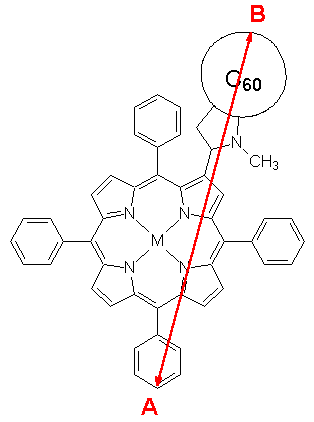
Figure 8. Definition of the cavity radius a.
The tenth excited state at 3.64 eV is the electron transfer state where an electron is transferred from the porphyrin donor to the fullerene acceptor This state is essentially described as the HOMOà LUMO and HOMO-1à LUMO one-electron transition. The P+-C60 – state has a large formal dipole moment of 42.7 D. Its value decreases when the center-to-center distance d both increases or decreases by rotation away from the optimized geometry at a=62° (see Table II.). For a=30°, corresponding to d=9.4Å, a dipole moment of m=36.6 D and for a=100°, corresponding to d=10.6Å, a dipole moment of m=39.7 D is calculated. The energy of the charge separated state is hardly affected by rotation (DE=3.53 eV for a=30°, DE=3.64 eV for a=60° and DE=3.67 eV for a=100°).
The solvent stabilization as a function of the rotation angle a and thereby different cavity radii a are estimated applying the formula of Lippert (2). The cavity radius a is defined as half the distance between the two carbon atoms A and B, as shown in Figure 8. The numbers for the radii are a=7.1Å (a=30°), a=7.5Å (a=62°), and a=8.0Å (a=100°), respectively, with the results summarized in Table II. The maximum dipole moment at a=62° has a surprising effect on the properties of the charge separated state in solution. The stabilization in energy in acetonitrile is computed to be 2.04 eV for the optimized structure (a=62°), 1.65 eV for a=30°, and 1.39 eV for a=100°. The corresponding numbers in benzene as an apolar solvent are 0.62 eV (a=60°), 0.53 eV (a=30°), and 0.44 eV (a=100°). The maximum dipole moment at a=62° yields the largest stabilization in total energy for both solvents. The charge separated state at a=30° has a smaller cavity radius and thereby a larger solvent stabilization only for dipole moment of a comparable number. The resulting higher charge separated state energy of the geometry with a=30° is due to the smaller dipole moment compared to that with a=62°. The larger dipole moment of the charge separated state at a=62° and the resulting larger solvent stabilization yields the lowest excitation energy in acetonitrile (DECS=1.60 eV) below the first excited state within the absorption spectrum, resulting in an efficient electron transfer. The energy is in the experimental region of 1.58 eV [8]. Thus, the dyad 1a is expected not to change its conformation in the charge separated state, as proposed recently for various bridged donor-acceptor systems [21]. The excitation energy DECS at a=62° is 3.02 eV in benzene and thus still above the first excited state energy of porphyrin character (DE=2.34 eV). An electron transfer will thus not take place, in agreement with experiment [8]. Comparable large dipole moments both in the electronic ground and excited states result in solvent stabilization energies for both the porphyrin and the fullerene excited states of less than 0.02 eV. No significant effect is ascertained on either the energies in the absorption spectrum or the energy differences of the porphyrin and porphyrin excited states relative to the ET state.
Table III.
Excitation Energies (DE in eV), Dipole Moments (m in D), Oscillator Strengths f, and Characterization of the First Excited Singlet States for the Metallated Dyad 1b. "Character" Describes the Main Configurations of the Excitations.
D E |
m |
f |
Character |
||
S1 |
P*-C60 |
2.18 |
5.6 |
0.000 |
HOMOà LUMO+6 HOMO-1à LUMO+4 |
S2 |
P*-C60 |
2.49 |
5.5 |
0.026 |
HOMOà LUMO+4 HOMO-1à LUMO+6 |
S3 |
P-C60* |
3.33 |
12.2 |
0.044 |
HOMO-2à LUMO |
S4 |
P-C60* |
3.35 |
8.2 |
0.003 |
HOMO-2à LUMO+1 |
S5 |
P+-C60- |
3.39 |
34.8 |
0.017 |
HOMOà LUMO |
S6 |
P-C60* |
3.44 |
7.9 |
0.001 |
HOMO-4à LUMO |
S7 |
P-C60* |
3.47 |
7.7 |
0.329 |
HOMO-3à LUMO HOMO-5à LUMO |
S10 |
P*-C60 |
3.67 |
8.9 |
1.483 |
HOMOà LUMO+4 HOMO-1à LUMO6 |
S16 |
P*-C60 |
3.86 |
17.5 |
1.247 |
HOMOà LUMO+6 HOMO-1à LUMO+4 |
The results for the characterization of the excited states of the zinc dyad 1b are summarized in Table III. In general, a deviation in energy of less than 0.1 eV is calculated for the fullerene excitations in comparison to 1a. This is a consequence of the similar character and energy of the fullerene orbitals of free-base tetraphenylporphyrin dyad 1a and the zinc dyad 1b (Figure 6). A larger dipole moment is computed for 1b compared to 1a in all excitations, where the HOMO-2 is involved. This is explained by the additional electron density at the porphyrin unit for the first occupied fullerene orbital, the HOMO-2, as shown in Figure 7. Thereby, partial charge transfer character is induced also in the C60 excited states, enhancing the dipole moment of the resulting state.
For 1b, the porphyrin frontier orbitals HOMO and HOMO-1 are destabilized, whereas the porphyrin LUMO´s are stabilized in energy in comparison to the free-base dyad 1a. The reduced energy gap yields in a decrease in excitation energy for the Q bands for the dyad 1b. A slight shift in absorption is observed in experiment [8]. The experimental observed Q bands at 2.09 eV and 2.23 eV are well reproduced by our calculations (2.18 eV and 2.49 eV, respectively). The computed oscillator strengths, dipole moments, and orbital contributions differ only marginally between the two investigated systems 1a and 1b for both the fullerene and porphyrin excitations. The energy of the charge transfer state in 1b is lowered by 0.25 eV to the S5 at 3.39 eV. An improvement in electron transfer character is thereby predicted for the zinc dyad.
![]()
4. Summary
An efficient energy and photoinduced electron transfer is observed in polar solvents like benzonitrile in a covalently linked free-base porphyrin-fullerene dyad and its zinc analogue. The single bond connecting both the donor and the acceptor subunits is quite flexible and the center-to-center distance varies by more than 1Å. The optimized geometry corresponds to a conformation with maximum dipole moment, resulting in the maximum solvent stabilization. The geometry of the charge separated state will thus be unchanged relatively to the ground state conformation. Applying the Lippert equation for relaxed solvent molecules, the charge separated state is stabilized in polar solvents to the first excited state. The calculated stabilization energy is not sufficiently in apolar solvents, explaining the absent electron transfer properties in different solvents. In addition, the excited states properties of these dyads are discussed with respect to the character of the molecular orbitals and electronic properties of the excited states involved. The energies of the transient states are calculated and comparison to experiment shows a good reproduction of absorption spectrum. The experimental observed low energy excited state of C60 is not found applying the semiempirical Hamiltonian. The electron donor property of the porphyrin subunit is strongly enhanced by insertion of a zinc atom. This is explained by a decrease in the energy gap of the four porphyrin frontier orbitals.
![]()
5. Acknowledgment
The German Academic Exchange Service (DAAD) is gratefully acknowledged for a Postdoctoral Fellowship.
![]()
6. References
- M. R. Wasielewski, Chem. Rev. 1992, 92, 435.
- H. Kurreck, M. Huber, Angew. Chem. 1995, 107, 929; Angew. Chem. Int. Ed. Engl. 1995, 34, 849.
- H. C. Hoch, L. W. Jelinski, H. G. Craighead, Nanofabrication and Biosystems, Cambridge University Press, Cambridge, 1996.
- D. Gust, T. A. Moore, Top. Curr. Chem. 1991, 159, 103.
- P. Liddell, J.P. Sumida, A.N. Macpherson, L.Noss, G.R. Seely, K.N. Clark, A.L. Moore, T.A. Moore, D. Gust, Photochem. Photobiol. 1994, 60, 537.
- R.M. Williams, J.M. Zwier, J.W. Verhoeven, J. Am. Chem. Soc. 1995, 117, 4093.
- R.M. Williams, M. Koeberg, J.M. Lawson, Y.-Z. An, Y. Rubin, M.N. Paddon-Row, J.W. Verhoeven, J.Org. Chem. 1996, 61, 5055.
- D. Kuciauskas, S. Lin, G.R. Seely, A.L. Moore, T.A. Moore, D. Gust, T. Drovetskaya, C.A. Reed, P.D.W. Boyd, J. Phys. Chem. 1996, 100, 15926.
- T.D.M. Bell, T.A. Smith, K.P. Ghiggino, M.G. Ranasinghe, M.J. Shepard, M.N. Paddon-Row, Chem. Phys. Lett., 1997 268, 223.
- D. Gust, T.A. Moore, A.L. Moore, D. Kuciauskas, P.A. Liddell, B.D. Halbert, J. Photochem. Photobiol. B: Biology 1998, 43, 209.
- D. K Kuciauskas, P.A. Liddell, S. Lin, T.E. Johnson, S.J. Weghorn, J.S. Lindsey, A.L. Moore, T.A. Moore, D. Gust, J. Am. Chem. Soc. 1999, in press.
- T.Clark, A. Alex, B. Beck, J. Chandrasekhar, P. Gedeck, A. Horn, M. Hutter, B. Martin, G. Rauhut, W. Sauer, T. Schindler, T. Steinke, VAMP6.1, Oxford Molecular Ltd. Oxford, 1998.
- M.J.S. Dewar, E.G. Zoebisch, E.F. Healy, J.J.P. Stewart, J. Am. Chem. Soc. 1985, 107, 3902.
- T. Clark, J. Chandrasekhar, Israel J. Chem. 1993, 33, 435.
- D. Majumdar, R. Sen, K. Bhattacharyya, S.P. Bhattacharyya, J. Phys. Chem. 1991, 95, 4324.
- A. Parusel, J. Mol. Model. 1998,4, 366.
- M. Gouterman, G.H. Wagniere, L.C. Snyder, J. Mol. Spectrosc. 1963, 11, 108.
- D. Gust, personal communication.
- Z. Gasyna, P.N. Schatz, J.P. Hare, T.J. Dennis, H.W. Kroto, R. Taylor, D.R.M. Walton, Chem. Phys. Lett. 1991, 183, 283.
- R. Bauernschmitt, R. Ahlrichs, F.H. Hennrich, M.M. Kappes, J. Am. Chem. Soc. 1998, 120, 5052.
- M.J. Shepard, M.N. Paddon-Row, J. Phys. Chem. A 1999, 103, 3347.