Investigation of the variables substitution methods to solve the
photochemical kinetics problems
Samuil Kh. Aranson, Leonid A. Belyakov, Sergei V. Zelentsov
Chemical Department, Nizhnii Novgorod State University
Gagarin Ave., 23. Nizhnii Novgorod, 603600, Russia
E-mail: zelen@ichem.unn.runnet.ru
The transition from natural for the photochemical kinetics coordinates, x, the distance
from the surface irradiated with u.v. light to the layer in which the photochemical
reaction having place, - t, irradiation time, to the coordinate system, E, intensity of u.v.
light irradiating the layer, - A, the concentration of the photochemically active
substance was used as the method of the exact solving of the photochemical kinetics
problems such as 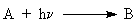 and (
and (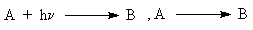 ). It
was shown that such a transition makes it possible to transform the PDE systems in
(x,t) coordinates into sets of the transcendental algebraic equations systems in the (E,A)
coordinates. The latter algebraic equations can be easily solved with the iterative
methods. The conditions of the direct and reverse transformations existence and of
their mutually eligibility were found out.
). It
was shown that such a transition makes it possible to transform the PDE systems in
(x,t) coordinates into sets of the transcendental algebraic equations systems in the (E,A)
coordinates. The latter algebraic equations can be easily solved with the iterative
methods. The conditions of the direct and reverse transformations existence and of
their mutually eligibility were found out.
1. Introduction
This work devoted to continuation of the studies began in [1-4] of methods of solving of the photochemical kinetics equations
describing the reactions in the media with restricted mobilities of reagents. For 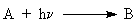 and (
and (
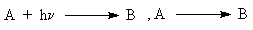 ) reactions (named as reactions 1 and 2) , the mathematical models of the processes
can be written as
) reactions (named as reactions 1 and 2) , the mathematical models of the processes
can be written as
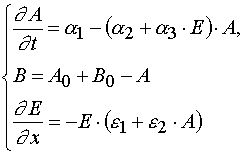 (1)
(1)
The parameters of the models in the system (1) are given in the Table 1.
Table 1.
Parameters of the mathematical models
Here 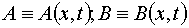 are the current concentrations of A and B substances having starting values A0 and B0,
respectively ( in [M m-3]).
are the current concentrations of A and B substances having starting values A0 and B0,
respectively ( in [M m-3]). 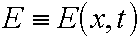 is intensity of the u.v. light at depth of x from the irradiated surface (in [W
m-3]) and E0 being the value at x=0. j is an effective photochemical reaction constant, ( in [j-1 m2]).
is intensity of the u.v. light at depth of x from the irradiated surface (in [W
m-3]) and E0 being the value at x=0. j is an effective photochemical reaction constant, ( in [j-1 m2]). 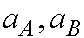 are
the absorbencies of A and B, ( in [M-1 m2]).
are
the absorbencies of A and B, ( in [M-1 m2]). 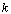 is the reaction constant of a thermally initiated reaction of the first order, ( in
[s-1] ). t is the current time, (in [s]).
is the reaction constant of a thermally initiated reaction of the first order, ( in
[s-1] ). t is the current time, (in [s]).
In the systems (1) x and t are independent variables, and A, B, E are the dependable variables. The initial and boundary
conditions are
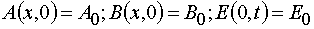 . (2)
. (2)
The systems (1) can be solved with different methods: (1) with the Picard iterative method; (2) using the transformation from
the (x,t) independent variables to the (E,t) independent variables [2-4]. In this work we propose to consider the system (1)
not in (x,t) coordinates but in (E,A) one.
In the first part of the article the exact solutions of (1) in the (E,A) coordinate system will be obtained and an attempt to make
the reversal transform will be made. In the second part of the article the existence and uniqueness problems for such
transforms will be studied.
2. Transformation (x,t)  (E,A) as the method of solving
(E,A) as the method of solving
Let us transform (1) from the (x,t) coordinates to the (E,A) ones. Then we have
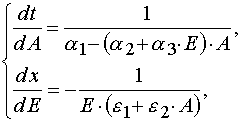 (3)
(3)
with the initial and boundary conditions imposed
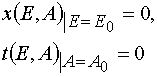 (4)
(4)
Solving (3) as ODE system having the initial and boundary conditions such as (4), one can obtain the exact solutions
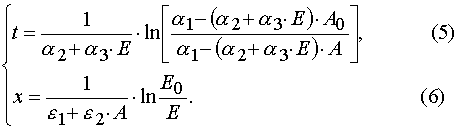
Algebraic transformations of relations (5) and (6) give the system of the transcendental algebraic equations.
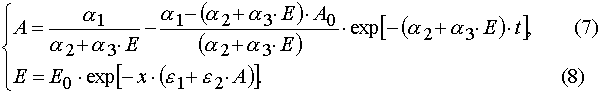
Eq (7) and (8) can be solved with the iterative method. For the first approximation one can take
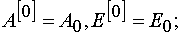 (9)
(9)
The first approximation can be written as

where
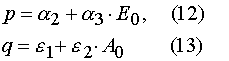
The second approximation is appeared to be
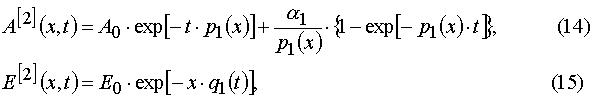
where
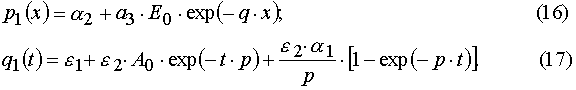
For the third approximation one could write
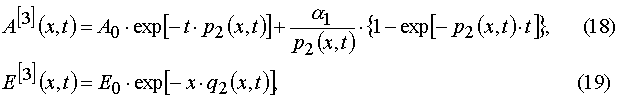
where
etc.
Thus, it is possible to obtain a solution of the system of the algebraic equations with any desirable precision. It is possible to
show that the iterative process has good convergence to the true solutions.
3. Finding out the conditions which have to be fulfilled to ensure the existence of the direct (x,t)
 (E,A) and reverse, (E,A)
(E,A) and reverse, (E,A)  (x,t) transformations.
(x,t) transformations.
To state the existence and mutual non-ambiguousness of the transformations (x,t)  (E,A) and (E,A)
(E,A) and (E,A)  (x,t) it is
desirable to study the Jacobian of the transformation
(x,t) it is
desirable to study the Jacobian of the transformation
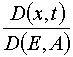
For analyzing of the Jacobian let us write an obvious relation
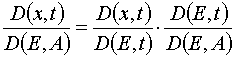 (22)
(22)
To obtain the exact form of (22) we have to prove the following lemma.
Lemma 1.
At 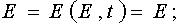 for system (1) there is determined mutually unambiguous and mutually continuous
transformation from the independent variables (E,t) to independent variables (x,t), in the case of reaction 1 the
variables E,A being in ranges
for system (1) there is determined mutually unambiguous and mutually continuous
transformation from the independent variables (E,t) to independent variables (x,t), in the case of reaction 1 the
variables E,A being in ranges 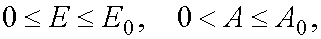 and in the case of reaction 2 being in
the
and in the case of reaction 2 being in
the 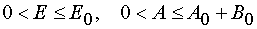 ranges.
ranges.
Proof
Eq (1) has the following form in (E,t) variables
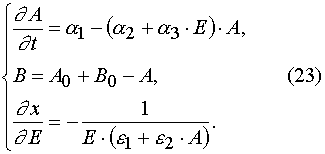
with the initial and boundary conditions imposed
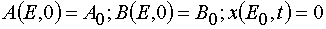 (24)
(24)
Let us calculate the Jacobian of the transformation from (E,t) to (x,t) variables. It has place  E(x,t), t
E(x,t), t  t..
t..
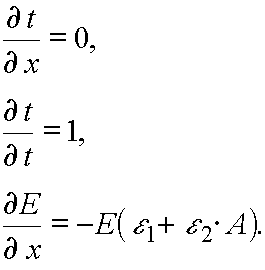
Hence
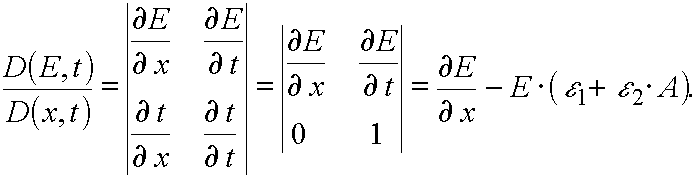 (25)
(25)
So as for all 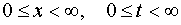 there have place inequalities
there have place inequalities 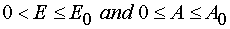 (for reaction
1) and
(for reaction
1) and 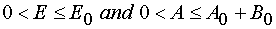 (for reaction 2), in the both reactions
(for reaction 2), in the both reactions 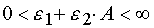 .
.
In other words, for all 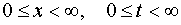 Jacobian
Jacobian
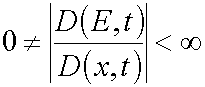
Having this in mind, one can conclude that a mutually unambiguous and mutually continuous transformation from (E,t) variables
to (x,t) ones is justified for in the case considered. So lemma 1 is proved.
Further we have to investigate Jacobian
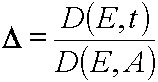
If it is the case when it will not be equal to zero or ¥ then due to lemma 1 both (E,t)  (E,A) and (x,t)
(E,A) and (x,t)  (E,A) transformation has place, they are mutually unambiguous and continuous. However there can exist the critical manifolds
W 1 from P : 0 < E £ E0 and 0 < A £ A0 for reaction 1 and W 2 from P : 0
< E £ E0 and 0 < A £ A0 + B0 for reaction 2 where Jacobian D ¹ 0 or ¥ . In the last
case mutually unambiguous and mutually continuous transformation from the (x,t) to the (E,A) independent variables is justified
only in the manifolds P * = P \ W 1 and P * = P \ W 2, for reactions 1 and
2, correspondingly. The latter forces us to initiate an additional investigations of the critical manifolds.
(E,A) transformation has place, they are mutually unambiguous and continuous. However there can exist the critical manifolds
W 1 from P : 0 < E £ E0 and 0 < A £ A0 for reaction 1 and W 2 from P : 0
< E £ E0 and 0 < A £ A0 + B0 for reaction 2 where Jacobian D ¹ 0 or ¥ . In the last
case mutually unambiguous and mutually continuous transformation from the (x,t) to the (E,A) independent variables is justified
only in the manifolds P * = P \ W 1 and P * = P \ W 2, for reactions 1 and
2, correspondingly. The latter forces us to initiate an additional investigations of the critical manifolds.
At first let us calculate the Jacobian of the transformation from (E,A) to (E,t). So as E  E and A
E and A  A(E,t), then
one has
A(E,t), then
one has
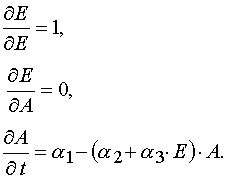 .
.
Hence
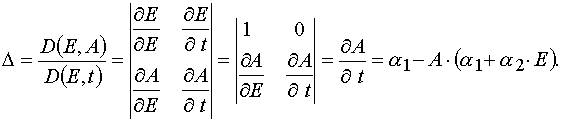 (26)
(26)
Let us investigate the case when 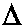 ¹ 0 and
¹ 0 and 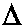 ¹ ¥ .
¹ ¥ .
Reaction 1.
For further investigation of determinant (26) let us prove lemma 2.
Lemma 2.
For all 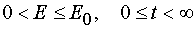 in the case of reaction 1 there is determined mutually unambiguous and
mutually continuous transformation from the independent variables (E,t) to the independent variables (E,A), and
there have place
in the case of reaction 1 there is determined mutually unambiguous and
mutually continuous transformation from the independent variables (E,t) to the independent variables (E,A), and
there have place 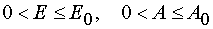 .
.
Proof.
This lemma can be proved by calculation of the determinant (26).
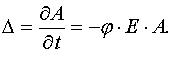
Taking into account that j ¹ 0, E > 0 and A > 0, one can prove that D < 0. To the other hand as
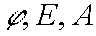 are limited D must be limited, too. So lemma 2 is proved and the transformations from (E,A) to (E,t)
and from (E,t) to (E,A) are justified.
are limited D must be limited, too. So lemma 2 is proved and the transformations from (E,A) to (E,t)
and from (E,t) to (E,A) are justified.
In an explicit form the transformations can be written as the following.
1) The transformation from (E,t) to (E,A) when 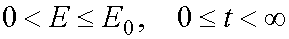 .
.
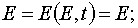 (27)
(27)
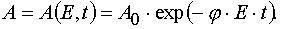 (28)
(28)
2) The transformation from (E,t) to (E,A) when 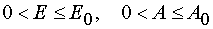
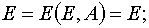 (29)
(29)
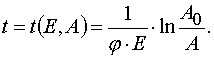 (30)
(30)
Theorem 1.
For all  in the case of model 1 there is determined a mutually unambiguous and mutually
continuous transformation from the independent variables (x,t) to the independent variables (E,A) when
in the case of model 1 there is determined a mutually unambiguous and mutually
continuous transformation from the independent variables (x,t) to the independent variables (E,A) when
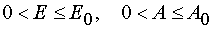 .
.
The proof of the theorem follows from lemma 1 and 2.
Consequence of the theorem can be formulated as following.
The critical manifold W 1 from the manifold of the possible values of the valuables of model 1 P
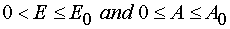 is empty, and W 1 ¹ Æ .
is empty, and W 1 ¹ Æ .
Reaction 2.
Due to the eq 26 the Jacobian is limited for all E and A from the manifold of the possible values
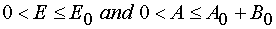 . Let us investigate the conditions when it is zero.
. Let us investigate the conditions when it is zero.
Theorem 2.
To do Jacobian be equal zero in the case of reaction 2 it is necessary and enough to require that the critical manifold
be defined as
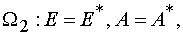
where
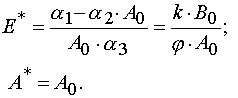
Proof.
Necessity condition.
Let us denote A*(E) to be values of A for which the Jacobian is zero. Taking into account eq 26 and Table 1 one can obtain
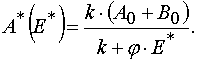
Using the latter definition and equation for A(E,t) it is possible to obtain the equation for calculation of E* values.
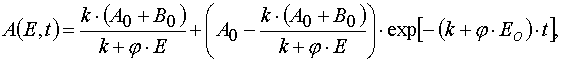
As a result we have
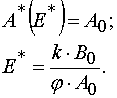
Sufficiency conditions.
Let us prove that when E = E* and A = A* then 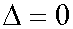 .
.
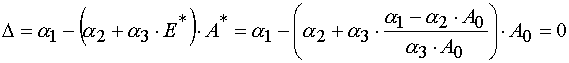
The latter proves the sufficiency condition.
An important consequence of the theorem 2 is the statement that for all E and A from P : 0 < E £ E0 and 0 <
A £ A0 excluding the point W 2 = (E*,A0) in the case of reaction 1 there is determined mutually unambiguous
and mutually continuous transformation from the (E,t) independent variables to the (E,A0 ones, and the transformation has the
following form
E = E(E,t) = E, (33)
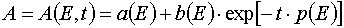 , (34)
, (34)
where
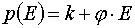 ,
,
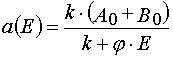 ;
;
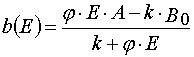 .
.
The reverse transformation from the (E,A) to the (E,t) independent variables has the following form
E = E(E,A) = E, (35)
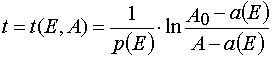 . (36)
. (36)
3. Discussion of the results .
The transformation from the (x,t) coordinates to (E,A) and reverse one for the models studied exists and mutually unique with
exception the point when Jacobian is equal zero. But this critical point corresponds to the quasi-stationary state, and the
intensity of u.v. light irradiation and concentration of substance A in the state are given by eq 31 and 32. So for this point there
exists a decision and the unique one, too.
Our solutions given by eqs (14)-(21) give us an opportunity to find u.v. light intensity and concentrations of reagents for
irradiation time, t, and at depth of a layer, x. However we usually can register experimentally only the dependencies E(t) and
A(t) for the given film thickness, h. So we have to deal with an average concentration
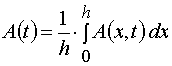
and an average intensity
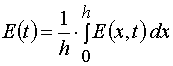
only. Assuming A(x,t) = A[2](x,t) and E(x,t) = E[2](x,t), let us calculate these averages.
Reaction 1.
Using parameters from Table 1 and taking into account Eqs (14)-(17) and formula presented in Appendix A, one can obtain
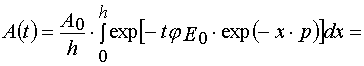
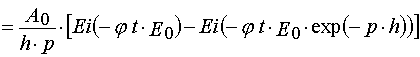 (37)
(37)
 (38)
(38)
where
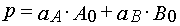
Reaction 2
In the case of reaction 2 the same transformations give
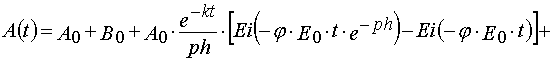
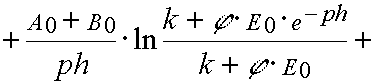
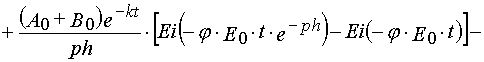
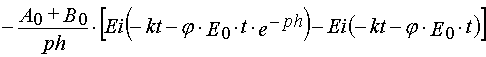 (39)
(39)
and
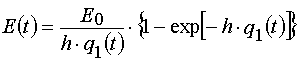 (40)
(40)
where
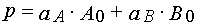
Formula (37)-(40) may be used to determine kinetics parameters from experimental kinetical curves. It is important that for
the latter we can use both dependencies, A(t) and E(t). The latter has special importance in the case when the absorption
spectra of A and B overlaps considerably, and so it is impossible to separate their contributions into E(t) accurately.
Acknowledgment. The work was done under financial support of Scientific Program "Russian University - Basic Researches"
(project 015.05.01.38), INTAS (project No.97-1843, 97-0804), RFBR (project No. 99-01-00230, 99-01-00231).
References
1. S.Kh.Aranson, L.A.Belyakov, S.V.Zelentsov, A.V.Oleinik. Analytical solution of kinetical equations describing the u.v.
exposure in photolithography // Proc. of Nizhnii Novgorod State University on Mathematical Modeling and optimal operation.
1998. No.2(19).P.90-109.
2. S.Kh.Aranson, L.A.Belyakov, S.V.Zelentsov, A.V.Oleinik, V.D.Lebedev. Investigation of mathematical models of
photochemical kinetics using differential form of Buger – Lambert -Beer // Book of Abstracts of the 5th Intern. Conf. on
“Non-linear vibrations in mechanical systems”. Nizhnii Novgorod. 13-16 Sept. 1999. Nizhnii Novgorod.1999.P.9-10.
3. S.Kh.Aranson, L.A.Belyakov, S.V.Zelentsov, A.V.Oleinik, V.D.Lebedev Analytical solution of photochemical kinetics
equations // Proc. of Nizhnii Novgorod State University on Mathematical Modeling and optimal operation. 1999.
No.2(21).P.98-108.
4. S.Kh.Aranson, L.A. Belyakov, S.V.Zelentsov, V.D. Lebedev ,New approach to the photochemical kinetics in the systems
with restricted mobilities// The 2nd Internet Conf. on Photochemistry. (http://www.photobiology. com/ photobiology99, paper
No.50).
Appendix A.
Calculation of the integrals.
1. Simple transformations can give the following chain.
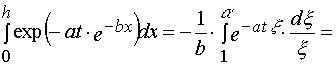
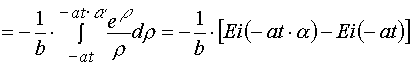 , (A.1)
, (A.1)
where
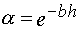
2. Integral
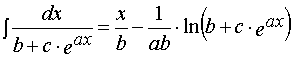 (A.2)
(A.2)
is well known and can be found in any Handbook in Mathematics.
3. Simple transformations can give the following chain.
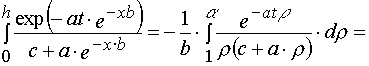 (A.3.1)
(A.3.1)
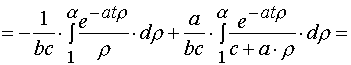 (A.3.2)
(A.3.2)
 (A.3.2)
(A.3.2)
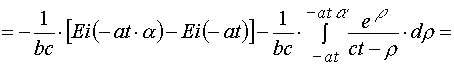 (A.3.3)
(A.3.3)
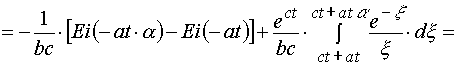 (A.3.4)
(A.3.4)
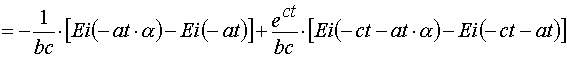 (A.3)
(A.3)
where

and (
). It was shown that such a transition makes it possible to transform the PDE systems in (x,t) coordinates into sets of the transcendental algebraic equations systems in the (E,A) coordinates. The latter algebraic equations can be easily solved with the iterative methods. The conditions of the direct and reverse transformations existence and of their mutually eligibility were found out.
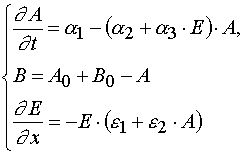 (1)
(1)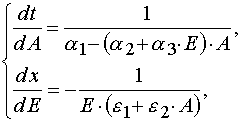 (3)
(3)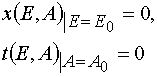 (4)
(4)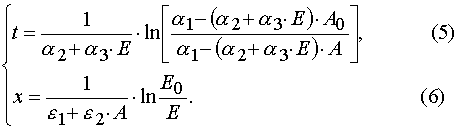
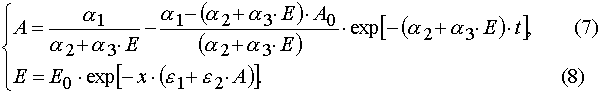

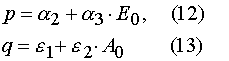
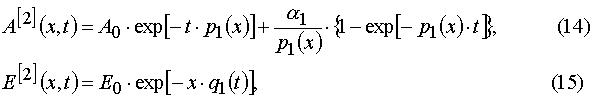
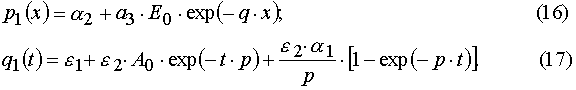
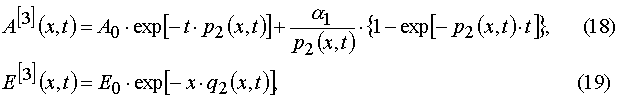
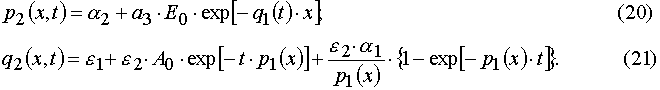
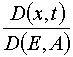
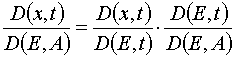 (22)
(22)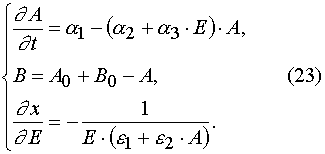
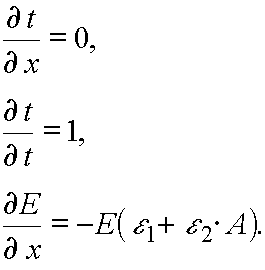
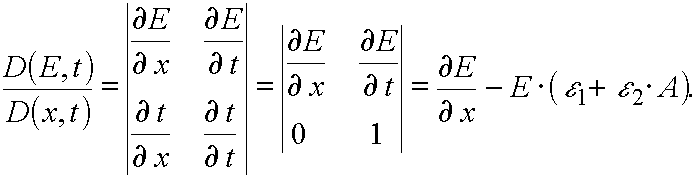 (25)
(25)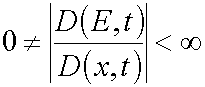
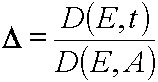
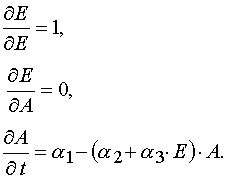 .
.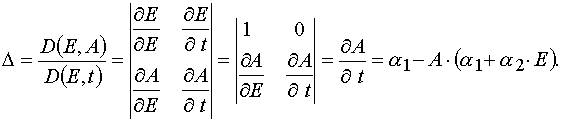 (26)
(26)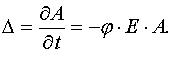
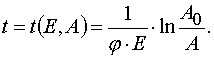 (30)
(30)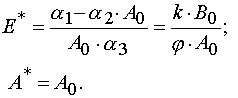
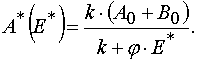
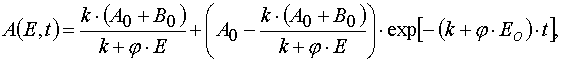
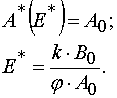
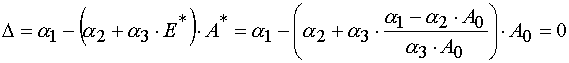
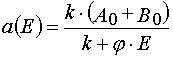 ;
;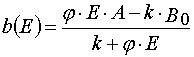 .
.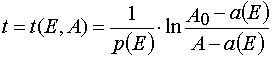 . (36)
. (36)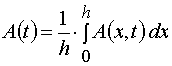
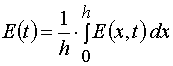
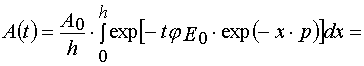
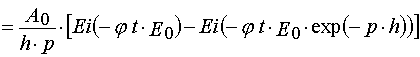 (37)
(37) (38)
(38)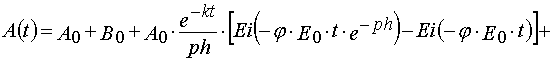
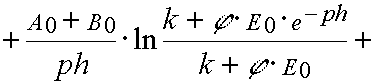
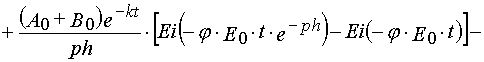
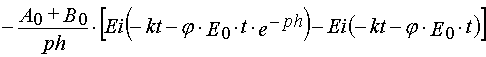 (39)
(39)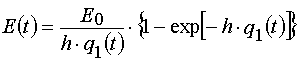 (40)
(40)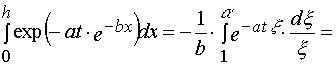
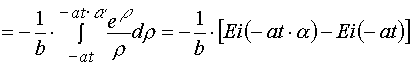 , (A.1)
, (A.1)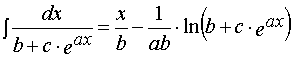 (A.2)
(A.2)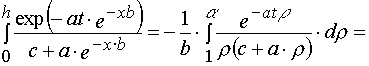 (A.3.1)
(A.3.1)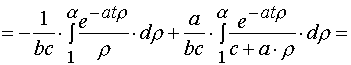 (A.3.2)
(A.3.2) (A.3.2)
(A.3.2)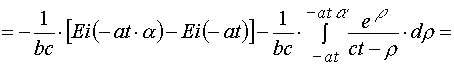 (A.3.3)
(A.3.3)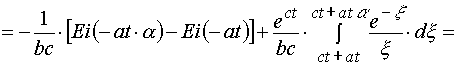 (A.3.4)
(A.3.4)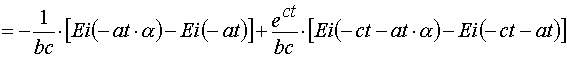 (A.3)
(A.3)