A Semiempirical Study of the Optimized Ground and Excited State Potential Energy Surfaces of Retinal and its Protonated Schiff Base

Andreas B. J. Parusel[a]^,* and Andrew Pohorille

NASA Ames Research Center, MS 239-4, Moffett Field, CA 94035; fax: (650) 604 1088.

Abstract

The electronic ground and first excited states of retinal and its Schiff base are optimized for the first time by the semiempirical AM1 Hamiltonian. The barrier for rotation about the C₁₁-C₁₂ double bond is characterized by variation of both the twist angle d(C₁₀-C₁₁-C₁₂-C₁₃) and bond length d(C₁₁-C₁₂) and the potential energy surface is obtained by variation of both parameters. A ground state rotational barrier of 15.6kcal/mol for retinal and 20.5kcal/mol for its Schiff base is calculated. The all-trans conformation is more stable by 3.7kcal/mol compared to the 11-cis geometry. For the first excited state, the 90° twisted geometry represents a saddle point for retinal with a rotation barrier of 14.6kcal/mol. In contrast, this conformation is an energy minimum for the Schiff base that easily can be reached at room temperature separated by a rotation barrier of only 0.6kcal/mol. This 90° minimum conformation is more stable by 8.6kcal/mol compared to the all-trans minimum. The character of the ground and first excited singlet states reveals the necessity for inclusion of double excitations into the calculations. We thus are able to present a reaction path on the S₁ surface of the retinal Schiff base with an almost barrierless geometrical relaxation into a twisted minimum geometry as observed in experiment.

1. Introduction

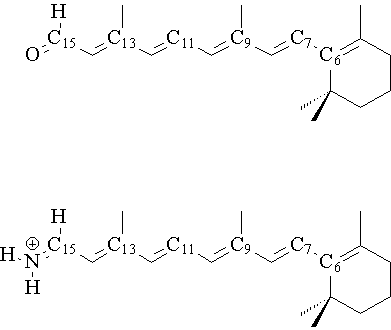
Structure of retinal (a, top) and its Schiff base (b, bottom) showing numbering of atoms.

The halobacteria Halobacteria halobium is able to convert light energy into chemical energy. These organisms normally grow in aerobic, saline environments. At low oxygen concentration and high light intensity, the bacteria cells form patches of a purple membrane on their surface, which also contains the photoactive protein bacteriorhodopsin (BR). BR is able to use the visible spectrum of light to generate a transmembrane proton gradient coupled via ATPase for the synthesis of ATP by the bacterium. In the middle of the protein, the active chromophore retinal (1) is located. Retinal is covalently linked in its all-trans form by a protonated Schiffs base (2) and a lysine residue with the protein. (For structure and numeration of atoms see Figure 1) Upon irradiation, the 13-cis isomer of BR is formed[1]. Rhodopsin is another retinal protein which is a visual pigment containing the 11-cis isomer of retinal as chromophore. When rhodopsin absorbs a photon, the chromophore isomerizes very fast (in the femtosecond region[2]) to the all-trans form. Now, the photon signal is reserved in form of a conformational change within the chromophore like a molecular switch. The ground and photoexcited molecular states exhibit distinctly different optical characteristics such as absorption and refraction index, and thus can be used to store date in a holographic fashion. Reversing the reaction by illumination with light of a different wavelength will erase the recorded data and make the system reusable. However, holograms recorded in the wildtype form of bacteriorhodopsin (isomerization in position 13) in have a short lifetime of milliseconds to seconds and that of rhodopsin (isomerization in position 11) of femtoseconds. For the application of data storage, one requires the data to remain permanently recorded until actively erased. The 11 and 13-cis isomers return rapidly to the ground state, while the 9-cis isomer remains in the excited state sufficiently long, making it more useful for permanent data storage[3].

It now is the main objective to identify specific genetic variations of the retinal chromophore resulting in modifications to the photocycle discouraging conversion to the 13- and 11-cis states while favoring conversions to the 9-cis state. The mechanism of this specific property of the photoisomerization has been studied intensively but is not completely understood yet (see e.g. ref. [4] for theoretical and ref. [5] for experimental studies, and references therein). A key theme in understanding the driving force towards isomerization in a particular position is to determine the exact potential energy surface for the twisting of the chromophore and to find the effect of the protein binding simulated by the Schiffs base. The choice of a method for calculating ground and excited state rotation barriers of a double bond is not quite clear either. A MRCI study of the 2,4-Pentadien-1-iminium cation[6] reveals that “…semiempirical methods give inaccurate energies for all rotational barriers in the electronic ground and excited states … [but] ab initio calculations agree relatively well”. Dekhytar and Rettig[7] on the contrary find that for rotation of merocyanines upon twisting the double bond “…the results provided by the [semiempirical] AM1 procedure are thus verified by the comparison with high-quality ab initio calculations”. We are thus confronted with two opposing opinions about application of semiempirical methods for studying the rotation about a C=C double bond.  However, for a detailed investigation of the isomerization process of retinal and its Schiff base, we decided to use a semiempirical methodology motivated by the following arguments: (1) Paizs and coworkers[8] have shown that protonated Schiff polyene bases with a different number of double bonds show significant differences in rotation barriers. A direct comparison of pentadiene-type to retinal-type polymer rotation barriers is not possible. The complete retinal system has to be included, which cannot be treated by ab initio and multi-reference methods. (2) More than 100 geometries have to be calculated for each electronic state considered when studying an energy surface with two variables. This cannot be accomplished by a high-quality method. (3) The effect of geometrical relaxation after photoexcitation needs to be included by optimization of the decisive electronic excited states and the important electron correlation effects have to be considered, too. Semiempirical methods in combination with a configuration interaction (CI) scheme are the only method of choice available nowadays fulfilling these requirements.

In this work we focus on the isomerization of retinal (1) and its Schiff base (2) in 11 position from the all-trans to the 11-cis conformer and we plan to extend the study to the rotation about both the 13 and 9 position in forthcoming publications. In the first part of the paper, the ground and excited state conformation of 1 and 2 are studied using the semiempirical AM1 Hamiltonian. Further semiempirical optimizations of both the electron ground, first and second excited singlet states are used to examine the rotation barrier of both systems by variation of the torsion angles and bond length. The environmental effect of the protein is simulated by linkage in a Schiff base and its energies and rotation barriers are compared to free retinal.

2. Computational Methods

The semiempirical program package VAMP version 7.0[9] is used for all calculations employing the AM1[10] Hamiltonian. The excited state geometries are optimized starting with the ground state optimized geometry with configuration interaction including all single and pairwise double excitations from the five highest occupied orbitals to the five lowest unoccupied orbitals (PECI=10)[11]. For the potential energy surface of both the ground and excited state, the rotation about the C₁₁-C₁₂ bond (for numeration, see Figure 1) is considered characterized by the twist angle d(C₁₀-C₁₁-C₁₂-C₁₃). This state is mainly of biradical character for orthogonal subunits (d»90°). We thus described the distribution of two electrons over two orbitals for the description of the rotation motion. The C₁₁-C₁₂ bond length d stretches simultaneously with increasing rotation angle d. The energy hyper-surface is calculated by a simultaneous variation of both the twist angle d and bond length d in steps of 10° and 0.01Å, respectively, from d=-10° to +190° and d=1.30Å to 1.50Å.

3. Results

3.1 Optimized Geometries

Table 1: Bond lengths [Å] of retinal and the protonated Schiff base

a)     ref. [12]

b)     DFT(B3LYP)/6-31G** calculations from ref. [15]

c)      This work

The polyene-aldehyd chain of retinal 1 is planar in its electronic ground state with the all-trans conformation (DH=4.9kcal/mol) more stable by 3.7kcal/mol relative to the 11-cis conformation (DH=8.6kcal/mol). Both methyl groups are bent out of the polyene plane only by a few degrees (9-position: AM1: 2.3°, exp: 4.9°, 13-position: AM1: 0.3°, exp: 0.6°) in perfect agreement with experimental data[12]. The bond lengths are of highly alternating character (see Table 1). The out-of-plane vibration motion of both methyl groups are of low frequency character. A free inversion motion from +50° to -50° is possible at room temperature (DDH < 0.5 kcal/mol). The lengths of the double bonds are calculated to be 1.35Å, the single bonds to 1.44Å-1.46Å. The calculated bond lengths are in very good agreement with experimental data[13] with an average deviation by 0.012Å from crystal structure bond lengths. Our semiempirical structure is in better agreement with experimental data compared to that of recently published high-quality DFT(B3LYP)/6-31+G*[14] and DFT(B3LYP)/6-31+G**[15] geometries. The cyclohexenyl unit is twisted out of the plane by 51.7°, which also is in excellent agreement with experimental rotation angle of 58.4°12 and slightly better than the result of 46.0° as obtained by a density functional theory based method15. The optimized first excited state of (1) is 67.6 kcal/mol higher in energy compared to the ground state. The planarity of the alkylene chain remains in the S₁ state but both the aldehyde group and the methyl groups are bent out of the alkene-plane in the same direction by 27° (aldehyde), 30° (methyl group in 9-position), and 17° (methyl group in 13-position).

The results for the Schiff base (2) differ somewhat from those of all-trans retinal (1). The C₁₅-C₁₄ and C₁₄-C₁₃ bonds are located closely to the aldehyde unit of 1. They are of double and single bond character, respectively. In the Schiff base, both bond lengths are 1.40Å, which is right between a typical single and double bond length. The distances become more similar to those of retinal for larger distances from the C=N unit and the C₅-C₆ bond length is 1.35Å in both systems. These results are in agreement with a recently published semiempirical PM3 study of a protonated retinyl-idene Schiff base[16]

3.2 Ground State Rotational Barrier of 1 and 2

Figure 2

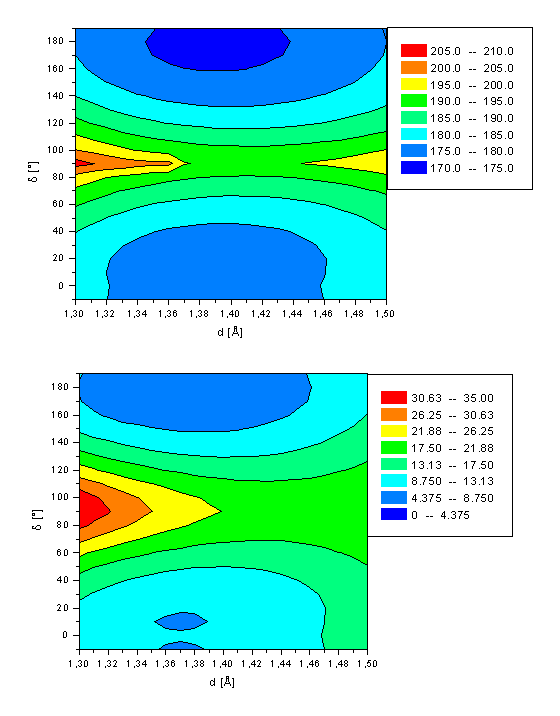Ground state energy of retinal (a, top) and its Schiff base (b, bottom) as a function of both the twist angle d(C₁₀-C₁₁-C₁₂-C₁₃) and bond length d(C₁₁-C₁₂).

The ground state potential energy surface for isomerization of retinal (1) and its Schiff base (2) are shown in Figure 2 and the energies for the stationary points are summarized in Table 2. The rotational angle d(C₁₀-C₁₁-C₁₂-C₁₃) and length d(C₁₁-C₁₂) are varied as the main geometrical parameters in steps of 10° from d=-10° to d=+190° and Dd=0.01Å from d=1.30Å to d=1.50Å, respectively (For a definition of d and d, see Figure 1) corresponding to a all-trans to 11-cis isomerization. All other degrees of freedom are optimized independently. The ground state global minimum of both 1 and 2 is in its all-trans form with a bond length of 1.37Å and an energy of 4.90kcal/mol (1) and 173.96kcal/mol (2). The 11-cis conformation is about 3kcal/mol higher in energy (1: 3.65kcal/mol 2: 2.88kcal/mol) with a small torsion angle of d=±10°. However, the planar conformation with d=0° is only 0.3kcal/mol higher in energy, which is less than the thermal energy available at room temperature. Both minima are characterized by approximately 90% by a closed shell electron distribution, i.e. full occupancy of the HOMO and an unoccupied LUMO. The transition state for isomerization at d=90° has a longer C₁₁-C₁₂ bond length of 1.45Å for retinal only. In the Schiff base, just a slight stretching by 0.02Å (d=1.39Å) is calculated. The energy barrier for isomerization from the more stable all-trans to the 11-cis conformation (11-cisàall-trans) in the electronic ground state is calculated to be 15.6kcal/mol (12.0kcal/mol) for 1 and 20.5kcal/mol (17.2kcal/mol) for 2. The transition state with orthogonal oriented subunits is characterized by an electron configuration different from that of the planar structure. The lowest singlet state of retinal at d=90° is characterized by a single electron transition from the HOMO into the LUMO. In contrast, the lowest singlet state of the Schiff base at d=90° is mainly a closed shell system, as for the two minima conformations. The contribution of the HOMOàLUMO transition at this twisted geometry is only 15% (see Table 2). The calculated AM1 rotation barrier of 20.5kcal/mol for 2 is compared to the calculated barrier of 55.3 kcal/mol of a recently published sa-CASSCF(6-31G) study[17]. This energy barrier is more than twice of our AM1 barrier. However, we consider our number being more reliable, due to the small active space of six electrons distributed among five active orbitals as employed in this work. Retinal and its Schiff base have six conjugated double bonds and thus a minimum of twelve p electrons has to be included in the active space to correctly describe the isomerization process. In CAS calculations of polyenes, the number of active orbitals should at least be equal to the number of p centers, which equals 12 in the case of retinal. Another argument for the reliability of our rotation barrier is the MO study of Paizs8 and coworkers who investigated the rotation barrier of the polyene Schiff base in 13-position. For a polyene Schiff base with four double bonds a rotation barrier of 55.4kcal/mol is calculated using CAS-SCF(4x4) (i.e. four electrons distributed over four active orbitals) and CAS-SCF(6x6), respectively. This barrier is significantly reduced to 43.2kcal/mol employing a larger active space of eight electrons and eight orbitals for the same system (CAS-SCF(8x8)). The rotation barrier further decreases for a protonated Schiff base with six double bonds (B3LYP: DH=29.5kcal/mol) relative to the system with three double bonds (B3LYP: DH=48.2kcal/mol). The thermal isomerization of 11-cis retinal has been studied by Hubbard, who observed activation energies in the range of 22.4-26.2kcal/mol[18]. A all-transà11-cis isomerization barrier for 2 of 28.31kcal/mol is obtained by Birge and Hubbard[19] using the semiempirical INDO-CISD approach which also is in much better agreement with our data. Molteni and coworkers4 determined a retinal isomerization barrier in the electron ground state of 17kcal/mol for the 11-cis à all-trans isomerization. This energy fits perfectly to our calculated energy of 17.2kcal/mol. The results in ref. 4 are obtained using the N-methylated Schiff base of retinal. However, their results differ only slightly to ours of the protonated Schiff base, as a direct comparison of the results of 2 with those of the N-methylated Schiff base show (results not shown).

Table 2 Energies (DH in kcal/mol) of the decisive geometries of retinal (1) and the protonated Schiff base (2) in its electronic ground (S₀), first (S₁) and second (S₂) excited singlet state with the decisive twist angle d (in °) and bond length d (in Å). The rotation barrier DDH (in kcal/mol) represents the energy barrier from the all-tans and 11-cis minimum conformation, respectively, to the stationary point at d=90° with Sad denoting a saddle geometry. The characterization of the singlet states is given with the electron configurations of contributions larger than 10% and the main configuration marked bold.

3.3 Excited State Rotational Barrier of Retinal (1)

Figure 3

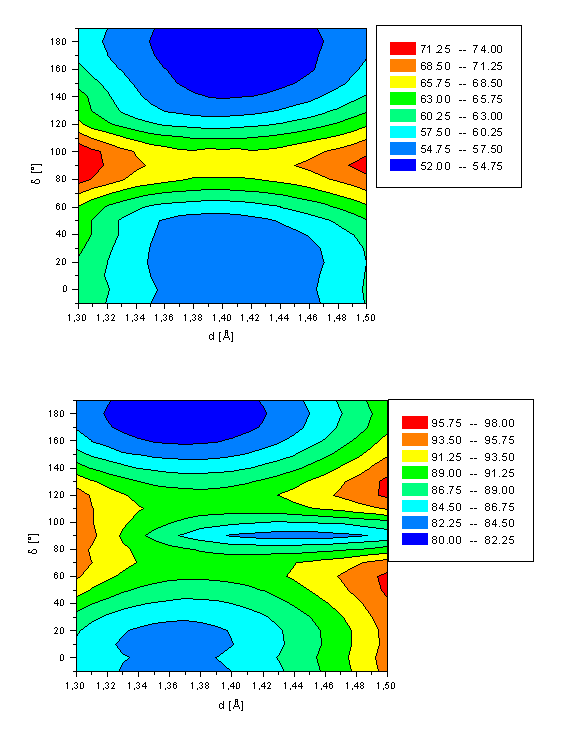First (a, top) and second (b, bottom) excited state energy of retinal (1) as a function of both the twist angle d(C₁₀-C₁₁-C₁₂-C₁₃) and bond length d(C₁₁-C₁₂).

The potential energy surface for isomerization of retinal (1) in its first and second excited singlet state are shown in Figure 3. The main parameters and energies are summarized in Table 2. A minimum is computed for retinal in its first excited state for both the all-trans and 11-cis conformation similar to the ground state. The all-trans form is more stable by 2.4kcal/mol and the 11-cis conformer is slightly distorted from planarity by d=30°. A rotation barriers of 14.6kcal/mol and 12.1kcal/mol is calculated for the all-trans à 11-cis and 11-cis à all-trans pathway, respectively. These barriers are comparable to those for the ground state of DH(180°-90°)=15.6kcal/mol and DH(10°-90°)=12.0kcal/mol. For both S₁ energy minima a significantly stretched C₁₁-C₁₂ bond length of d=1.41Å is computed. The saddle point at 90° has a bond length d of only 1.38Å, which is only slightly longer than for the ground state (d=1.37Å). The S₁ minima are mainly characterized (>40% contribution) by a double excitation from the HOMO into the LUMO with two smaller contributions (~20% each) of a HOMOàLUMO and HOMO-1àLUMO one electron transition. The saddle point at d=90° is best described (contribution of 82%) by an electron configuration with both HOMO MO’s occupied and all virtual orbitals unoccupied, representing the electron distribution for the electronic ground state of 1 in both the all-trans and 11-cis minimum geometry. The AM1 calculations thus corroborate the existence of a conical intersection between the S₀ and S₁ in the twisted conformation region of 1 as postulated by the CASSCF/PT2 calculations of Garavelli and coworkers[20].

The two energy minima structures of the second excited state of retinal (d=10° and d=180°) are best described by a HOMOàLUMO transition (~80%). The conformation at d=90° is a third energy minimum for d(C₁₁-C₁₂)=1.44Å. The twisted molecule is of comparable energy (DH=83.4kcal/mol) as the local minimum at d=10° with DH=83.6kcal/mol. The energy barrier for the all-trans à 11-cis rotation is calculated to be 9.6kcal/mol (all-transà11-cis) and 6.4kcal/mol for the 11-cis à all-trans pathway, respectively. Both energies are significantly smaller than for the rotation in both the ground and first excited state. No energy minimum is observed for the bond length d fixed to its equilibrium length of 1.36Å. A two-dimensional cut of Figure 3a at d=1.36Å reveals a saddle point at d=90° with a rotation barrier of 6.9kcal/mol (DH(d=180°-d=90°)) and 3.7kcal/mol (DH(d=10°-d=90°)), respectively. This clearly  demonstrates the necessity of including the bond length d into the computations.

3.4 Excited State Rotational Barrier of retinal Schiff base (2)

Figure 4

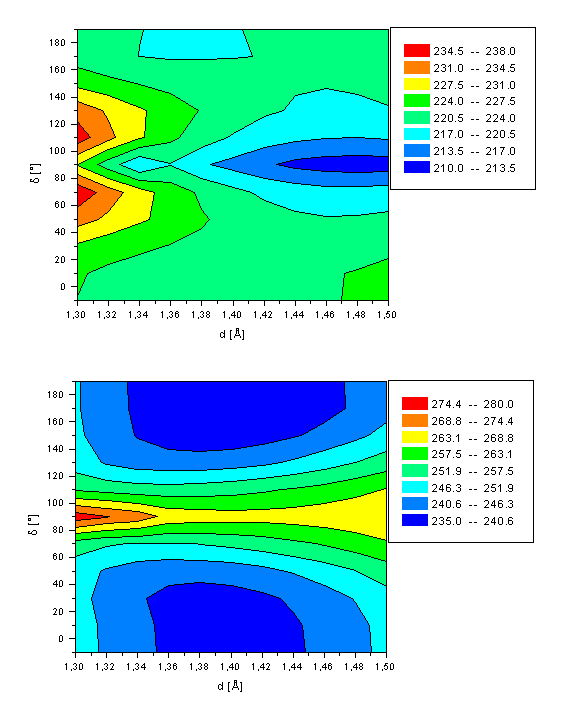First (a, top) and second (b, bottom) excited state energy of the retinal Schiff base (2) as a function of both the twist angle d(C₁₀-C₁₁-C₁₂-C₁₃) and bond length d(C₁₁-C₁₂).

A different situation is found for the excited state hyper-surfaces of 2 (see Figure 4). A minimum in energy is computed for a twisted C₁₁-C₁₂ bond (d=90°) and d=1.48Å (DH=211.7 kcal/mol) for the first excited state. The main difference to 1 originates from a different characterization of the S₁ state at this conformation, which is mainly (75%) of single excited character of a HOMOàLUMO excitation. Thus, the conical intersection as calculated for retinal does not exist in the Schiff base. Both local minima at d=10° and d=180° are approximately 10kcal/mol higher in energy, and characterized by a double excitation of two electrons from the HOMO into the LUMO, similar to retinal. The calculated rotation barrier of 0.5kcal/mol and 0.6kcal/mol (all-transà11-cis and 11-cisàall-trans reaction path, respectively) is similar to the thermal energy available at room temperature. Thus, even at gas phase condition the Schiff base is able to relax spontaneously after photoexcitation by rotation about the C₁₁-C₁₂ double bond into the global S₁ minimum with orthogonal orientation of both subunits. The C₁₁-C₁₂ bond length is more of single bond than of double bond character (d=1.48Å). Significantly larger stabilization energies are expected in protein environment. The second excited state of 2 is of HOMOàLUMO single excitation character for the region around the all-trans and 11-cis minima, comparable to retinal. The twisted geometry of the Schiff base in its second excited state is mainly (41%) described by a single excitation of one HOMO electron into the LUMO+2 (for retinal: LUMO+1). No energy minimum is observed, as has been found for retinal in its second excited singlet state. The rotation barrier of ca. 30kcal/mol is significantly higher than the rotation barrier in the electronic ground state of ca. 20kcal/mol.

3.5 Discussion

Our semiempirical results are compared and discussed with respect to the results of the recently published DFT study of retinal and its Schiff base by Molteni et al4. The authors treat the electronic ground state by the well established density functional theory with the BLYP functional and Troullier-Martins norm-conserving pseudopotentials. A HOMOàLUMO single excitation is assumed to characterize the first excited singlet state. The excited states are modeled within a variational density functional theory scheme. Their computed ground state 11-cisàall-trans isomerization barrier for the Schiff base (2) of 17kcal/mol is in perfect agreement with our rotation barrier of 17.2kcal/mol. In contrast, Molteni et al. calculate the ground state rotation barrier for 11-cisàall-trans isomerization of retinal 1 at a significantly higher energy of 24kcal/mol (AM1: 12.0kcal/mol). This discrepancy originates from a different characterization of the ground state at the saddle point (d=90°) conformation. The DFT barrier results from a characterization of this transition state by a closed shell system, whereas the AM1 method determines a conical intersection. Thus, the ground state is best described by an electron configuration of one electron promoted from the HOMO into the LUMO and we thereby calculate a much smaller rotation barrier. The good agreement with the DFT results of Molteni and coworkers for the rotation barrier of the Schiff base is easily explained: Both the DFT and AM1 method characterize the d=90° conformation as a closed shell structure. Consequently, a rotation barrier of comparable size is computed. ´

Molteni and coworkers4 calculate an excited state rotation barrier of approximately 5kcal/mol for the retinal isomerization, significantly smaller than for the ground state. According to our opinion, there are two main problems with this result and its interpretation: First, our AM1 calculations reveal the character of the first excited state of double HOMOàLUMO excitation and not of a single HOMOàLUMO one-electron transition as assumed by Molteni et al. The AM1 calculations determined the second excited state of this HOMOàLUMO character. Comparable to the DFT study, a much smaller rotation barrier of 6.4kcal/mol is calculated for this S₂ state (ref. 4: 5kcal/mol). Second, the character of the first excited state differs for d=90° compared to that of d=0° and d=180°. A sufficiently large number of excitations has to be included into the calculations for a correct description of the first excited state. Taking into account different electron distribution at different geometries.

Molteni and coworkers calculate a rotation barrier of 14kcal/mol for the 11-cisàall-trans isomerization of the Schiff base in its first excited state. According to their results, the d=90° geometry is a saddle point. On the contrary, the AM1 method locates an energy minimum at this geometry. The main reason for this difference is the different description of the S₁ state of 2: AM1 characterizes the first excited state of 2 by a double excitation from the HOMO to the LUMO at geometries away from the twisted conformation (d¹90°). Only the decoupled geometry (d=90°) is described by a HOMOàLUMO transition. Molteni and coworkers describe the complete energy surface by this HOMOàLUMO one electron excitation. The S₂ state as calculated by the AM1 method is mainly of this HOMOàLUMO transition. One would thus expect a AM1 rotation barrier for the S₂ state comparable to the S₁ barrier as obtained by Molteni. However, we calculate a much larger rotation barrier of 27.8kcal/mol. This higher energy results from a characterization of the d=90° structure by a one-electron transition from the HOMO into the LUMO+2. This MO is of higher energy and the larger energy gap to the HOMO explains the larger rotation barrier.

4. Conclusion

In this theoretical study we have investigated the isomerization of both retinal and its Schiff base in its electronic ground state and excited states (S₁ and S₂) by the semiempirical AM1 method. All geometries have been optimized independently. The aim of this study has been to explain the experimentally observed barrierless isomerization process of Bacteriorhodopsin as it occurs in nature.

The ground and first excited state energy surface of retinal (1) is characterized by a high rotation barrier of 15.6kcal/mol (S₀) and 14.6kcal/mol (S₁) with an energy maximum at d=90° for rotation about the C₁₁-C₁₂ double bond. The second excited state has a local minimum at d=90° separated from the two planar minima by a barrier of 9.6kcal/mol, which is too high to be overcome at room temperature. A reversed shape of the S₁ and S₂ energy surfaces is computed for rotation about the C₁₁-C₁₂ double bond for the Schiff base (2). The first excited state shows a minimum at d=90° that is separated from the planar all-trans minimum by a significantly smaller energy barrier of 0.6kcal/mol. Thus, the experimentally observed fast and efficient photoisomerization of Bacteriorhodopsin[21] can be attributed to a spontaneous relaxation of the Schiff base in its first excited state. The ground state of 2 is of closed shell character for all geometries, but for retinal 1 a conical intersection is detected at d=90°. Here, the system is of HOMOàLUMO singly excited character. The first excited state of both systems is characterized mainly by a HOMOàLUMO double excitation for all geometries except in the region around d=90°. Here, a closed shell electron configuration is calculated for 1 but a HOMOàLUMO singly excited character for 2, explaining the differences in the energy hyper surfaces of both system. Thus, both double and higher excitations have to be included in the CI space in order to correctly characterize the first excited singlet state of retinal and its Schiff base.

Acknowledgment

AP acknowledges the German Academic Exchange Service (DAAD) for financial support by a postdoctoral fellowship.

5. References