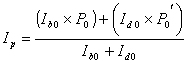Estimation of pedestrian level UV-B exposure under trees in suburban environments

R.H. Grant¹, G.M. Heisler² and W. Gao³

1.       Dept. of Agronomy, Purdue University, W. Lafayette, IN, USA

2.       USDA Forest Service, Northeastern Research Station, Syracuse, NY, USA

3.       Natural Resources and Ecology Laboratory, Colorado State University, Fort Collins, Colorado, USA

Abstract

Solar ultraviolet radiation is associated with a wide range of human health problems including skin cancer, cataracts, and immune deficiencies.  The health risk of UV radiation is evident by the creation in many countries of a UV Index to provide the public with an estimate of the risk for erythema (sunburn) each day.  Trees influence the amount of solar UV radiation that reaches pedestrians.  In open tree canopies, where the spacing between trees is equal to or greater than the width of individual tree crowns, the irradiance is strongly dependent on the relative positions of the individual trees and the point of interest in or under the canopy.  Analysis of measurements with broadband sensors showed that the relative irradiance in the UV-B was a function of both sky view and solar zenith angle.  A three-dimensional model was developed to predict the UV-B irradiance fields in open tree canopies.  The model showed that the locations people typically perceive as shady, low-irradiance locations in the environment actually can have significant UV-B exposure (40-60% of that in the direct sunlight).  An evaluation of the model showed it was able to predict the relative irradiance (fraction of above-canopy irradiance) under both sunlit and shaded conditions with a mean bias error of less than 0.01 and a root-mean-square error of 0.07.  Applying the model to determine the relationship of tree cover in residential neighborhoods to erythemal UV-B exposure for children and adults during the fours hours around noon for June and July showed that exposures at cities with 15^o and 30^o latitude are nearly identical.  For latitudes between 15^o and 60^o latitude, sun protection factors (SPF) were less than 2 for less than 50% tree cover.  An SPF of 10 was possible at all latitudes for tree cover of 90%.  Maximal protection from erythemal UV-B occurs when one is in shade and negligible sky is visible.

Introduction

      Solar UV at the earth's surface has many implications for human health.  Erythema is caused primarily by the UV-B portion of the solar spectrum (280- 315 nm) and to a smaller extent by UV-A (315- 400 nm).  Sun exposure has been found to be associated with non-melanoma skin cancers (squamous and basal cell carcinomas, SCC and BCC) and cutaneous malignant melanoma (CM).  There is some evidence of different relationships with sun exposure (Vitasa et al., 1990), though both BCC and SCC are thought to be correlated with cumulative lifetime UV exposure (Lloyd et al., 1993).  Though medical opinions and epidemiological studies vary as to the relationship between sun exposure and CM  (Heisler and Grant 2000), the statement that “it is now well established that sun exposure is one of the probable causes” (Diffey and Saunders, 1995) is generally accepted by the research community.  These health effects may be exacerbated by depletion of the stratospheric ozone layer and attendant increases in UV radiation. (deGruijl, 1995, Madronich and deGruijl, 1994).  Although changes in habits of recreation, dress, and the increased value placed on a “tan” are evidently largely to blame for most of the increases in skin cancer rates (Long et al., 1996), these rates are expected to increase by approximately 2% for every persistent 1% loss in average ozone concentration (deGruijl, 1995). 

The human health impact of solar UV at the earth's surface depends on the environmental conditions as well as human habits.  Most people do not play out their lives in open fields but reside and work in environments in which there is significant obstruction to sky and direct sun due to buildings and vegetation.  Significant improvements in the prediction of open-environment exposure of surfaces at various slopes have been made in the past 10 years (Parisi and Wong, 1994; McKenzie et al., 1997; Grant, 1998).  Prior studies have shown that the I_r (or relative irradiance) at pedestrian heights is significantly influenced by canopies of vegetation and buildings (Grant, 1997; Grant and Heisler, 1996; Brown et al., 1994).  The influence of canopy structures on irradiance in open tree canopies means that the canopy structure influences the UV exposure of people.  The mean tree cover of medium-size cities in Texas, Ohio, California, Kansas, Alabama, New York, and Pennsylvania range from less than 10% to 37% (Rowntree, 1984a,b).  Since the climatic region, population density, and socioeconomic characteristics of the population influence the tree canopy structure in urban areas, these factors also influence UV exposure.  Rowntree (1984a) suggested that cities in more humid subtropical climates typically having more tree canopy cover than northern continental climates, and drier climates having less tree cover than moister climates.  In a survey study of the tree cover of many cities, Nowak and coworkers (1996) indicate that tree cover in residential areas ranges from 48% in forested climates, to 27% in grassland climates, and 11% in desert climates.

One approach to evaluating UV exposure by populations in different neighborhoods is to model the relative irradiance as influenced by trees and buildings and utilize measured UV-B irradiance above the canopy to approximate the irradiance in pedestrian space under the canopy.  The above-canopy UV-B irradiance measurements can be derived from monitoring networks such as that of the USDA UV-B Radiation Monitoring Program (Bigelow et al., 1998).  This paper describes the development and verification of a 3-D model for use in predicting the UV-B irradiance in open tree canopies and applies the model to estimate dose exposure in residential suburban areas under cloud-free skies based on tree cover, latitude, day, time-of-day.  Suggestions as to the relative effectiveness of adding tree cover for the mitigation of erythemal UV-B exposure is also discussed.

Methods

The model developed to predict UV-B irradiance within and below vegetation canopies is an adaptation of a 3-D relative irradiance model (Gao, 1996, Gao et al., 2000).  This model assesses the UV-B irradiance below canopies given initial sky conditions and canopy composition and structure.  The canopy consists of a finite number of 3-D geometrical bodies with the individual plant sub-canopies (crowns) regarded as discrete scattering volumes of ellipsoidal shape.  The model calculates the irradiance at a point in the array of crowns with foliage in the crowns characterized by a single foliage density r but with the possibility of defining individual crown dimensions. 

The modeled relative irradiance (I_p) was determined by the modeling of the probability of penetration of both diffuse radiation (I _d0), and direct beam radiation (I_b0) according to:

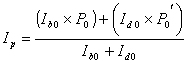                                                                                                             [1]

where P₀ is the probability that a direct beam of solar radiation ray will pass through the canopy un-intercepted, and P₀¢ is the probability that sky diffuse radiation will pass through the crown un-intercepted.  The incident (above-canopy) radiation was partitioned into diffuse sky and direct beam radiation according to the radiation models of Bird (1984) and Shippnick and Green (1982). 

The probability of a beam of radiation traveling, un-intercepted, from the beam’s source (inside or outside the canopy) to any given point in the array of subcanopies was defined as (Norman and Welles, 1983):

                                                                                                                                    [2]

where W is the direction from which the radiation is coming (with zenith angleand azimuth j), G(W) is the fraction of foliage area that is projected towards the source of radiation, r is foliage density (foliage area per unit canopy volume), and S is the distance through the canopy that the ray must pass. 

In our model, the computation of the distance, S, that a ray passes through a discrete plant volume is calculated assuming all radiation sources are on a reference plane above the canopy.  The penetration probability of the direct beam radiation through the canopy is based on the Poisson distribution of canopy elements (leaves) in the crowns. The probability of penetration of sky diffuse radiation is computed as:

                                                                    [3]

where N is the sky radiance for a given zenith angle  and azimuth angle j.  For cloud-free skies, the sky radiance is modeled according to Harrison and Coombes (1988) in the short wave waveband (SW;300-3000 nm), Grant et al. (1996) in the photosynthetically active radiation waveband (PAR; 400-700 nm), and Grant et al. (1997a) in the UV-A and UV-B wavebands.  Although not used in the present study, these references cited for cloud free skies also develop corresponding sky radiance distributions for translucent overcast  cloud cover have been developed by Coombes and Harrison (1988) for the SW, Grant et al. (1996) for the PAR, and Grant et al. (1997b) for the UV-A and UV-B.  For opaque overcast sky conditions, the sky radiance can be modeled according to Steven and Unsworth (1980) in the SW and Grant and Heisler (1997) in the PAR, UV-A, and UV-B.

Validation measurements

For model validation, the vegetation density of the crown was set to a high value to effectively prevent penetration of radiation through the tree crown and only cloud-free sky radiance distributions were used.  Scattering was not included in the model because: 1) there was only a small amount of reflecting surfaces not associated with the single tree used in the validation measurements, 2) crown r was set to be opaque, and 3) reflections off the single tree were largely off shaded surfaces.  The reflected energy off the shaded surfaces is small in the UV-A and UV-B due to the typically low (5-6%) leaf reflectance in the UV (Gao et al., 1996) and is small in the PAR and SW due to the low amount of available radiation for reflection off the shaded surfaces resulting from the typically small diffuse fractions of cloud-free skies in the PAR and SW.  An example of the estimated I_p array for four trees under a cloud-free sky with solar zenith angle of 30^o is illustrated in Figure 1.  Note that the pattern of 'shading' of I_p  by the individual crowns is relatively dispersed, with no distinct 'edges' to the 'shadow'.  This is a result of the great influence of sky radiation on the UV-B irradiance.

The model was validated for use in open canopies typical of suburban backyard situations by comparing model predictions with minimum values of broadband irradiance measurements made under generally cloud-free skies during 17 measurement periods in the summers of 1996, 1997 and 1999 at West Lafayette, Indiana, USA (40.5°N latitude) (Table 1).  The measured relative irradiance (I_r ) in or under the canopy was defined as:

                                                                                                                                            [4]

where I₀ is the above canopy irradiance and I_min is the minimum measured irradiance at a height of 1.4 m under the canopy.  Minimum values were chosen in the validation phase because the actual tree crown foliage density was not known and the measurements were chosen in locations that did not appear to have sunflecks in the shadow pattern.  Below-canopy irradiance sensors were in completely sunlit or completely shaded locations near a relatively isolated sweetgum (Liquidambar styraciflua) tree.  A shaded location was defined as having canopy biomass between the sun and the sensor position so as to minimize sunflecks on the sensors during the measurement period.  The UV-B irradiance in a park-like grove was also measured to determine if the extrapolation of the single-tree model validation also could apply to a complex array of trees (Table 2).  The grove consisted of large red oak (Quercus rubra), white ash (Fraxinus americana), Red Cedar (Juniperus virginiana) and red maple (Acer rubrum.) trees approximately 30 to 40 m in height.  The grove had a mean distance between trees of 13 m.  The mean values of the measurements were used in this analysis.  For both the single tree and the grove measurements, the above-canopy reference sensors were on a nearby building roof (with unobstructed view of the sky) within 150m to 300m of the measurement locations.

The irradiance measurements were made in the four wavebands: SW, PAR, UV-A, and UV-B .  SW irradiance was measured using Kipp-Zonen CM5 radiometers (spectral response bandwidth of 320 to 2500 nm).  The cosine response error of the CM5’s was less than 1% for solar zenith angles less than 75^o and the temperature error was –0.15%/^oC (Coulson, 1975).  The time constant of the sensor was approximately 4s (Latimer, 1972).  PAR irradiance was measured using Li-COR 190SA sensors (LI-COR Inc, Lincoln, NB) with a response bandwidth of 400 to 702 nm (LI-COR, 1986).  The cosine response error of these sensors was less than 5% for solar zenith angles between 20 and 60^o (LI-COR, 1986).  UV-A irradiance was measured using SED038/UV-A/W sensors (International Light, Inc., Newbury, MA, USA) with a spectral response of 314 to 388 nm (as reported by the manufacturer).  The UV-A sensor system had a laboratory-measured temperature error of -0.5 %/C and a cosine response error of less than 10% for solar zenith angles between 20 and 80^o (Grant, 1996).  UV-B irradiance was measured using SED240/UVB/W sensors (International Light, Inc.) with a spectral response of 258 to 315 nm  (as reported by the manufacturer).  The UV-B sensor system had a laboratory-measured temperature error of -0.3 %/C and a cosine response error of less than 30% for solar zenith angles between 20 and 60^o (Grant, 1996).  The laboratory-measured time constant for the IL sensors was less than 5 s.  In 1997 and 1999, the minimum erythemal dose (MED; McKinlay and Diffey, 1987) above the canopy was measured on the building roof (Table 1) using a UVB-1 sensor (Yankee Environmental Systems, Inc., Turners Falls, MA.).  This sensor had a spectral response bandwidth of 280 to 317 nm and a cosine response error of less than 10%.

All sensors were sampled at 5 to 30 s intervals for between 30 minutes and several hours per location.  Sensors were intercompared before the series of validation measurements and the recorded sensor response adjusted to provide equivalent response during the validation measurements.  Temperature response corrections were applied to the measurements prior to analysis.  No corrections for the cosine response error of each sensor were applied due to the complexity of the shade environment.  The lack of cosine correction likely resulted in overestimates of the relative UV-B irradiance. Irradiance measurements for each waveband were normalized by the measured flux density at the above-canopy reference location.

Upward facing hemispherical photographs from each measurement site were made using a Canon 7.5 mm lens.  The photographs were analyzed to determine total sky obscuration due to canopies for each 10° annulus, either by a grid of fine lines with 10° intervals in both azimuthal and zenithal directions or by analyzing digitized images of the photographs using Glic v2.0 developed by C. Canham (Institute of Ecosystem Studies, Millbrook, NY, USA).  In the manual analysis of photographs, an area of the sky hemisphere was defined as obscured if the sky was not visible at the intersection of the azimuthal and zenithal grid lines.  In the digital analysis of the photographs, the each pixel was evaluated for sky obscuration or visibility.  The sky view for the below-canopy measurement locations varied from 0.05 to 0.8 for measurements made near a single tree  (Table 1) and from 0.1 to 0.66 for measurements made in the tree grove (Table 2).

Model application scenarios

The model was used to predict the relative UV-B dose for various surfaces on a person randomly moving around in a tree-covered park near three major metropolitan areas of the USA.  The relative irradiance on the person in the park was estimated from the areal average I_p across a regular distributed 11 x 11 array of spherical trees with the cover fraction equivalent to literature values.  The I_p over a range of solar zenith angles was determined for cloud-free sky conditions, calculated at the height of the crown base (assumed pedestrian height) for a regular array of spherical crowns. 

One objective of the project was to provide a means to estimate UV-B exposure based on weather information and satellite of aircraft images of the area.  To link the tree cover interpreted from the imagery to the sky view from the ground, the model was run for the 11 x 11 array of opaque spherical tree crowns assuming an isotropic sky radiance distribution so that the diffuse irradiance fraction is equivalent to the skyview factor.  The mean skyview initially decreased rapidly with increasing tree cover until approximately 50% cover, then decreased more gradually with continued increase in the tree cover (Fig. 2).  The tree cover fraction and solar zenith angle were then regressed against the areal average I_p to provide a means to relate below canopy irradiance and dose to above canopy irradiance and dose for locations with a given latitude on a given day and time.  The relationship between the canopy cover fraction (the area of the ground divided by the area of canopy covering the ground by looking downwards into the canopy from directly overhead) and the sky view (a weighted area of sky visible from the ground when looking upwards through the canopy) was determined by setting the sky radiance function to a constant value and noting the diffuse-only relative irradiance.

Estimates of dose on people within the tree array were made for the 10AM to 2PM interval over the summer period of June through July at latitudes of 15 ^o, 30 ^o, 45 ^o, and 60 ^o.  The densities of the tree array were chosen to produce tree cover fractions of 0.1, 0.3, 0.5, 0.7, and 0.9.  The areal average I_p for a given solar zenith angle and tree cover fraction provided the relationship between the above and below canopy irradiance for the tree array.  The relationship between solar zenith and cloud-free sky erythemal UV-B (McKinley and Diffey, 1987) was based on an irradiance by solar zenith angle regression of the UVB-1 irradiance measurements for 22 June 2000 (ozone column of 274 DU; EarthProbe TOMS V.7 Archive Overpass data, http://jwocky.gsfc.nasa.gov/) from the USDA UV-B Radiation Monitoring Program network sites at Mauna Loa, Hawaii, USA (elevation 3397 m, latitude 19.5^o).  The cumulative daily dose for the 4-hr period centered on solar noon was described using the minimum erythemal dose (MED) defined by Parrish and coworkers (1982).  Measured erythemal UV-B values were adjusted to sea level using the mean ratio of sea level to 3400-m modeled irradiance (0.857) based on the Schippnick and Green (1982) model.

Results and discussion

Model Accuracy

The accuracy of the model to predict near-surface irradiance in the vicinity of a single tree was evaluated by comparing I_p to measured I_r for all four wavebands.  In general, the modeled values were greater than the measured values.  However, the variable density of the tree crown and the deviation of the tree crown shape from the modeled ellipsoid resulted in a larger fraction of sky penetrating through the oddly shaped crown and making the measured values sometimes greater than the modeled values.  The mean bias error of the model was 0.026 while the root-mean-squared error (RMSE) was 0.093 (n=92).  The model error was relatively insensitive to the magnitude of the measured I_r  (Fig. 3).  This is similar to the model accuracy reported by Gao et al. (2001), although the measured values used in their analysis were the mean values and not the minimum values used here.  Gao et al. (2001) found the model had mean bias errors of 0.038 and 0.033 for an apple orchard and maize canopies respectively.  The model RMSE was 0.082 and 0.061 for the apple orchard and maize canopies respectively (Gao et al., 2001).

The modeled I_p tended to overestimate the measured I_r at high solar zenith angles.  This was partly due to the decreasing ratio of direct beam to diffuse sky radiation with increasing solar zenith angle and partly due to lack of correcting the UV-B measured values for the cosine response error in the sensor response.  Excluding the UV-B measured values when the solar zenith angle was greater than 50 deg reduces the model error significantly (Fig. 3).  After omitting these values from the analysis, the mean bias error for the single-tree measurements to 0.004 with an RMSE of 0.068 (n=82).

Areal mean I_p  estimation

The areal mean I_p under the 11 x 11 regular array of spherical trees was determined for a range of solar zenith angles and tree cover fractions (Fig. 4).  In general, the higher the solar zenith angle, the closer the mean areal relative irradiance approached 1/(tree cover fraction).  The rate of change in mean areal relative irradiance with change in tree cover was greatest at low tree cover fractions and least at high fractions.

The dose received by pedestrians in the treed area was estimated by utilizing a time history of UV-B monitoring measurements from the USDA UVB Monitoring Network (Bigelow et al., 1998).  By associating the view factor with the canopy cover, areal mean exposure of people in vegetated locations can be estimated based on remotely-sensed tree cover.  The validity of this approach of estimating exposure based on tree cover for a canopy of trees was evaluated by comparison of the modeled minimum and maximum values with mean values measured in the grove of trees, which were distributed irregularly across the landscape.  The modeled mean areal I_p was then compared to the measured relative irradiance in the tree grove for specific sunlit and shaded sensor locations.  Figure 5 illustrates the individual I_r values relative to the mean areal I_p for shaded and sunlit areas for the grid of regularly distributed spherical trees using the relationship between sky view (measured) and tree cover fraction (modeled).  In general, shaded environments with small skyview had the lowest relative irradiance.  Areas near the single tree had I_r values of 0.5 to 0.3 (Fig. 5) corresponding to an equivalent SPF (sun protection factor) of 2 to 3.  Clearly, significant exposure of pedestrians is likely unless the tree cover has a nearly closed canopy.  The advantage of being in shade appears to decrease with increasing solar zenith angle, however it should be noted that the minimum erythemal dose at the higher solar zenith decreases to approximately 2 MED/hr by solar zenith angles of 45^o (Table 1). Results showed that the envelope representing the areal mean minimum (shade) I_p for solar zenith angles ranging from 15 ^o to 60^o approximated the mean of the observed values in the grove of trees as well as near the single tree (Fig. 3).  Values well above the shade areal mean I_p were in direct sunlight.  Variation around the areal mean shade I_p are expected, since point and area averages are being compared.

The multivariate regression of the mean areal I_p of the 11 x 11 array of trees for solar zenith angles of 15^o, 30^o, 45^o, and 60^o against the calculated tree cover fraction and solar zenith angle resulted in the relationship:

I_p = -.431 + 1.5787e^-M - 0.0435 ln(q)                                                                                    [5]

where M is the tree cover fraction and q is the solar zenith (adjusted r² = 0.97).  In general, I_p decreased with solar zenith angle and increased with tree density.

Dose estimation for residential areas

UV exposure during childhood is a risk factor in the development of skin cancers in adults.  Reducing the exposure of children and young adults therefore should reduce risk for later-life cancers.  Studies have shown that children in primary grades may receive greater UV exposure than those in secondary grades  (Diffey et al., 1996).  Diffey et al. (1996) attributed this difference in exposure to young children spending more time playing outdoors in open areas.  The exposure of children to UV-B between 10AM and 2 PM during the summer period of June and July was evaluated at four latitudes and six tree-cover fractions.  Since the above canopy irradiance for all simulations was only a function of the solar zenith angle, the variation in the daily dose at each latitude location was a result of the combined effect of latitude and canopy cover.

The estimated daily dose for a child playing during the four hours centered around solar noon varied from approximately 12 MED for cities at 60^o latitude to 22 MED for cities at 15 ^o and 30 ^o latitude (Fig. 6A).  The similarity between the exposure in cities at 15 ^o and 30 ^o latitude was due to the time of year chosen for the comparison (solar declinations of approximately 20^o).  The maximum MED for a given day was at the summer solstice for latitudes above 23.5^o while the exposure at 15^o latitude was nearly constant throughout the period (Fig. 6A).  Increasing tree cover decreases exposure.  The equivalent sun protection factor (SPF) of tree cover was less than 2 for tree cover of less than 0.5 at all latitudes (Table 3).  SPF values greater than 5 typically required tree covers of greater than 0.7, a relatively dense canopy.  The corresponding relationship between SPF and sky view (related to tree cover by Fig. 4) for shaded locations in the simulated 11 x 11 tree array illustrate the range of approximately 2 SPF units for solar zenith angles ranging from 15^o to 60^o degrees (Fig. 7).  While high tree cover minimizes the areal mean UV-B exposure and maximizes the areal mean SPF, careful choice of locations within an array of trees can result in high SPF while the tree cover is low.  Maximum benefits of any given tree cover can be had by minimizing the view of the sky by being in the shade and near individual trees of the array.  Grant (1997) showed that greater protection (SPF of 10) can be had by people if they stay under the tree crowns.  This corresponds with the SPF associated with most of the measurements made in the tree grove (Fig. 7).  The range of SPF values evident for a given skyview are a result of measurements being made under a range of solar zenith angles at similar locations in the vicinity of the single tree and in the tree grove.  It should be remembered that receptor surfaces on the human body have a wide range of orientations and the estimates described here apply only to an exposed vertex of the head.  Exposure to the face can be estimated using corrections for various orientations of the head and various parts of the head developed by Kimlin and Parisi (1999) and others.

One limitation of this approach is the limited availability of UV-B irradiance measurements within urban areas.  This is important because the UV-B irradiance within urban areas can be expected to differ from that of the surrounding rural area due to differences in the ground albedo and air pollution (Madronich et al., 1998, Grant et al., 2000).  As such, estimates of UV-B exposure of people in cities should be based on urban UV-B measurements (Grant et al., 2000).  This is an important area for development, as only a few cities in the USA have UV-B monitoring underway.

We have considered above only the UV-B exposure resulting from existing vegetation cover.  From an urban landscape planning point of view, how much tree cover is best to reduce UV-B exposure of pedestrians?  Although obviously the increase in tree cover always decreases exposure to UV-B (Fig. 6B), the change from no tree cover to 0.1 tree cover has a greater impact than the change from 0.9 to 1.0 cover.  Therefore planting some trees in an open area creates real sun protection benefits.  Because of the interplay of tree cover on skyview, there is an optimal value where the effect of the tree cover on reducing exposure is the greatest.  The relative effectiveness of planting trees to increase tree cover and reduce erythemal UV-B exposure for pedestrians was evaluated by comparing the fractional change in dose over the two-month exposure period to the fraction of tree cover.  Model results indicate that cities with low latitudes of 15^o to 30^o receive the maximum benefit of tree cover relative to UV-B exposure when the tree cover fraction is approximately 0.3 (Table 4).  For any given tree cover fraction, the greatest benefits of tree cover to mitigate UV-B exposure occur at high latitudes (Table 4). 

References

Bigelow, D. S., J. R. Slusser, A. F. Beaubien and J. H. Gibson  (1998)  The USDA Ultraviolet Radiation Monitoring Program, Bull. Amer. Meteor. Soc., 79, 601-615

Bird, R. E.  (1984)  A simple solar spectral model for direct-normal and diffuse horizontal irradiance.  Solar Energy 32, 461-471.

Brown, M. J., G. G. Parker and N. E. Posner  (1994)  A survey of ultraviolet-B radiation in forests. J. Ecol. 82, 843-854.

Coombes, A. W. and A. W. Harrison  (1988)  Angular distribution of overcast sky short wavelength radiance.  Solar Energy 40,161-166.

Coulson,K. L.  (1975)  Solar and terrestrial radiation. Academic Press, NY, NY 322p.

de Gruijl, F. R.  (1995)  Impacts of a projected depletion of the ozone layer.  Consequences 1, 1-10. [http://www.gcrio.org/CONSEQUENCES/summer95/impacts.html].

Diffey, B. L., C. J. Gibson, R. Haylock and A. F. McKinlay  (1996)  Outdoor ultraviolet exposure of children and adolescents. British J. Dermatol. 134, 1030-1034.

Diffey, B. L. and P. J. Saunders  (1995)  Behavior outdoors and its effects on personal ultraviolet exposure rate measured using an ambulatory datalogging dosimeter.  Photochem. Photobiol. 61, 615-655.

Gao, W.  (1996)  Modeling and measurement of ultraviolet irradiance in vegetation canopies. PhD Dissertation, Purdue University.

Gao, W., R. H. Grant and G. M. Heisler  (1996)  Spectral radiative properties of various tree species in ultraviolet wavelengths and the impacts on irradiance modeling and measurement. In Proceedings of the 22nd Conf. on Agricultural and Forest Meteorology, pp. 417-418, American Meteorological Society, Boston, MA, USA.

Gao, W., R. H. Grant, G. M. Heisler and J. R. Slusser  (2001)  A geometric radiation transfer model for vegetation canopies in the UV-B.  Agron. J. (submitted)

Grant, R. H.  (1996)  Characterization of UVA and UVB irradiance sensor systems. In  Proceedings of the 22nd Conf. on Agric. and Forest Meteorology,  pp. 169-172, American Meteorological Society, Boston, MA, USA.

Grant, R. H.  (1997)  Biologically-active radiation in the vicinity of a single tree.  Photochem. Photobiol. 65, 974-982.

Grant, R. H.  (1998)  Ultraviolet irradiance of inclined planes at the top of plant canopies.  Agric. Forest Meteorol. 89, 281-293.

Grant, R. H., W. Gao and G. M. Heisler  (1996)  Photosynthetically-active radiation: sky radiance distributions under clear and overcast conditions.  Agric. and Forest Meteorol. 82, 267-292.

Grant, R. H. and G. M. Heisler  (1996) Solar ultraviolet-B and photosynthetically active irradiance in the urban sub-canopy: a survey of influences. Int J Biometeorol 39, 201- 212.

Grant, R. H. G. M. Heisler and W. Gao  (1997a)  Clear sky radiance distributions in ultraviolet wavelength bands. Theor. and Applied Climatology. 56, 123-135.

Grant, R. H., G. M. Heisler and W. Gao  (1997b)  Ultraviolet sky radiance distributions of translucent overcast skies. Theor. and Appl. Climatol. 58, 129-139.

Grant, R. H. and G. M. Heisler  (1996)  Solar ultraviolet-B and photosynthetically-active irradiance in the urban sub-canopy. Int. J. Biometeorol. 39,201-212.

Grant, R. H. and G. M. Heisler  (1997) Obscured overcast sky radiance distributions for the ultraviolet and photosynthetically-active radiation wavebands. J. Appl. Meteorol. 36,1336-1345.

Grant, R. H., G. M. Heisler and J. Slusser  (2000)  Urban UV measurements: rationale for the establishment of long-term monitoring in the Baltimore Ecosystem Study.  pp. 195-196 In:  Proceedings of the 3^rd Symposium on the Urban Environment, 14-18 August, 2000, Amer. Met. Soc.

Heisler, G. M. and R. H. Grant  (2000)  Ultraviolet Radiation, Human Health, and the Urban Forest.  U.S. Dept. of Agric. Gen. Tech. Rep. NE-268.  Newtown Square, PA.  35 pp.

Harrison, A. W. and C. A. Coombes  (1988)  Angular distribution of clear sky short wavelength radiance.  Solar Energy 40, 57-63.

Ireland. W. and R. Sacher (1996)  The angular distribution of solar ultraviolet, visible, and near-infrared radiation from cloudless skies.  Photochem Photobiol. 63, 483-486.

Kimlin, M. G. and A. V. Parisi  (1999)  Effect of ultraviolet protective strategies on facial ultraviolet radiation exposure. in Proceedings- 15th International Congress of Biometeorology, Nov. 8-12, 1999, Sydney, Australia (CDROM, paper ICB19.2).

Latimer, J. R.  (1972)  Radiation Measurement., International Field Year for the Great Lakes ech. Manual Series No. 2, Secretariat, Canadian National Comm. For the Int. Hydrological Decade., Ottawa, Canada., 53p.

LI-COR  (1986)  LI-COR Terrestrial Radiation Sensors, Type SB.  Instruction manual.  Pub. 8609-58, LI-COR, Inc., Lincoln, NB. 25p.

Lloyd, S. A., E. S. Im and D. E. Anderson, Jr.  (1993)  Modeling the latitude-dependent increase in non-melanoma skin cancer incidence as a consequence of stratospheric ozone depletion.  In: Biggs, R. Hilton; Joyner, Margaret E.B., eds.  Stratospheric Ozone Depletion/UV-B Radiation in the Biosphere.  New York: Springer-Verlag.  NATO ASI Series I.  18, 329-337.

Long, C. S., A. J. Miller, H.-T. Lee, J. D. Wild, R. C. Przywarty and D. Hufford  (1996)  Ultraviolet index forecasts issused by the National Weather Service.  Bulletin of the American Meteorological Society.  77, 729-748.

Madronich, S. and F. R. de Gruijl  (1994)  Stratospheric ozone depletion between 1979 and 1992: Implications for biologically active ultraviolet-B radiation and non-melanoma skin cancer incidence.  Photochem. Photobiol. 59,541-546.

Madronich, S., R. L. McKenzie, L. O. Bjorn and M. M. Caldwell  (1998)  Changes in biologically active ultraviolet radiation reaching the Earth's surface. Journal of Photochemistry and Photobiology B: Biology,  46, 5-19

McKenzie, R. L., K. J. Paulin and M. Koltkamp  (1997)  Erythemal UV irradiances at Lauder, New Zealand: Relationship between horizontal and vertical incidence.  Photochem. Photobiol. 66, 683-689.

McKinlay, A. F. and B. L. Diffey  (1987)  A reference action spectrum for ultraviolet erythema in human skin.  CIE Journal. 6, 17-22.

Norman, J. M. and J. M. Welles  (1983)  Radiative transfer in an array of canopies.  Agron. J. 75, 481-488.

Nowak, D. J., R. A. Rowntree, E. G. McPherson, S. M. Sisinni, E. R. Kerkmann and J. C. Stevens  (1996)  Measuring and analyzing urban tree cover.  Landscape and Urban Planning.  36,49-57.

Parisi, A. V. and C. F. Wong  (1994)  A dosemetric technique for the measurement of ultraviolet radiation exposure to plants.  Photochem. Photobiol. 60, 470-474.

Parrish, J. A., K. F. Jacniske and R. R. Anderson  1982.  Erythema and melanogenesis action spectra of normal skin. Photochem. Photobiol. 36, 187-191.

Rowntree, R. A.  (1984a)  Ecology of the urban forest. Urban Ecology 8, 1-12.

Rowntree, R. A.  (1984b)  Forest canopy cover and land use in four eastern United States cities. Urban Ecology 8,55-68.

Schippnick, P. F. and A. E. S. Green  (1982)  Analytical characterization of spectral irradiance in the ,iddle ultraviolet, Photochem. Photobiol. 35, 89-101.

Steven, M. D. and M. H. Unsworth  (1980)  The angular distribution and interception of diffuse solar radiation below overcast skies.  Quart. J. R. Met. Soc., 106, 57-61.

Vitasa, B. C., H. R. Taylor, P. T. Strickland, T. Paul [and others]  (1990)  Association of nonmelanoma skin cancer and actinic keratosis with cumulative solar ultraviolet exposure in Maryland watermen.  Cancer  65, 2811-2817.

Table 1: Isolated tree measurement conditions.

Table 2: Tree grove measurement conditions

TABLE 3:  Sun protection factors for tree cover

TABLE 4:  Benefit of tree cover to erythemal UV-B exposure

Figure 1 – - Example of modeled relative irradiance array.  Plan view of the trees are indicated by the hatched circles.  Darker shading corresponds with lower I_p values.  The dark line in the shadow indicates the I_p =0.5 level.  The sun is coming from the bottom of the figure with a 30^o zenith angle.

Figure 2 –  Modeled relationship between tree cover and sky view.

Figure 3- Model accuracy- Panel A illustrates the relationship of model error to solar zenith angle for measurements made near the single tree .  Panel B illustrates the relationship of the model error to the magnitude of the measured relative irradiance.  Errors for periods when the solar zenith angle exceeded 55^o are indicated with filled symbols.

Figure 4 - Modeled relative irradiance for the 11 x 11 tree array.  The areal mean relative irradiance across the entire array for solar zenith angles of 15^o (filled circle), 30^o (filled triangle), 45^o (open diamond), and 60^o (open triangle) and the areal mean relative irradiance in the shade across the array for solar zenith angles of 15^o (dash-dot line), 30^o (dashed line), 45^o (long dashed line), and 60^o (solid line) are indicated.

Figure 5 – Comparative measurements and modeled relative UV-B irradiance -  Measured relative irradiance of shaded (open circles) and sunlit (open triangles) locations near the single tree and shaded (filled circles) and sunlit locations (filled triangles) in the tree grove are indicated.  The solid lines represent the domain between the modeled areal mean relative irradiance and areal mean shaded relative relative irradiance for the 11 x 11 array of trees for a solar zenith angle of 15^o.

Figure 6 - Estimated erythemal UV-B Dose for mid-day exposures during June and July.  Panel A illustrates the daily exposure above canopy for locations at four different latitudes.   Panel B illustrates the daily exposure for varying tree cover fractions at latitude 30^o.  

Figure 7 – Sun protection factors for shaded environments- Measured SPF values from the single tree (open circles) and tree grove (filled circles) are indicated.  The dashed lines indicate the mean Shade SPF for the 11x11 tree arrays.