QUANTITATIVE SPIN TRAPPING SUPPORTED BY CHEMICAL MECHANISM

András Németh, Tamás Kriska and Dezső Gál

Institute of Chemistry, Chemical Research Center, Hungarian Academy of Sciences, Pusztaszeri út 59-67, Budapest 1025, Hungary

dezso@cric.chemres.hu

ABSTRACT

The accumulation of adducts formed in the interaction between spin trap DMPO and cumylperoxyl as well as with 1-cyano-1-propylperoxyl radicals is investigated based on a detailed reaction mechanism. Comparison of the computed profiles of the adducts vs reaction time with measured data shows an acceptable agreement. It also demonstrates that the decomposition of the adduct during the initial period of the process can be neglected as is assumed in a novel method of quantification of spin trapping.

INTRODUCTION

It has been suggested earlier that free radicals formed in vivo (native free radicals, NFR) might contribute to photosensitization [1]. It has been shown by us [2] that the total concentrations of NFR in tumor cells of mice measured by ESR technique has been decreased in the presence of sensitizer triplets (³PS*) [3] similarly to our in vitro studies with macrophages where induced chemiluminescence (CL) diminished.

In an earlier publication [4] a novel method of quantification of spin trapping was described and the spin trap itself was considered as a specific inhibitor in the sense that the adduct formed undergoes decomposition. Experiments showed that during the initial time period the accumulation of spin adduct (formed between NFR and the spin trap) vs time can be assumed to be linear and, thus, consumption of adducts negligible. Further, it was assumed, that in the later period the consumption of the adduct is governed mainly by monomolecular, bimolecular and radical induced decomposition. Based on these assumptions the rate parameters of adduct formation between different oxygen centered radicals and di-methyl-pyroline-oxide (DMPO) as spin trap and of the mono- and bimolecular decomposition of the adducts have been determined by kinetic ESR spectroscopy. An attempt to obtain the rate constant of the radical induced decomposition of the adduct, however, proved to be unreliable.

The aim of the present investigation is to study that above approximations and the extent they affect the determination of the rate constants of the formation and decomposition of the adduct. For this purpose a detailed mechanism of the overall process is compiled and calculated product accumulations compared to experimental ones.

Formation of adducts of cumylperoxyl (RO₂) and 1-cyano-1-propylperoxyl radicals, (rO₂), with DMPO have been chosen as model processes. Accordingly, the corresponding mechanisms of the oxidation of azo-bis-iso-butyro-nitrile (AIBN) and of AIBN-induced oxidation of cumene have been investigated in both cases in the presence of DMPO, in chlorobenzene solvent and at 60^oC.

MATERIALS AND METHODS

Due to the rather complex nature of the overall processes, a hierarchical approach was used for the quantitative treatment of the reaction mechanism. It consists of dividing the complete reaction mechanism into "subsets" of reactions. These subsets were compiled starting from the smallest one by adding stepwise reactions to them. The sets comply with the requirement that each one is completely included into the succeeding level. It is also essential that well established rate parameters should be available to evaluate each subsystem separately. The advantage of this method is an improved accuracy.

The hierarchy of the systems is illustrated in Table 1.

Table 1. Subsystems of the oxidation of cumene initiated by AIBN

Accordingly the AIBN/DMPO/O₂ system is made up of 2 steps, first validating the AIBN/O₂ system and adding to them reactions involving DMPO and the resulting products. The AIBN/cumene/DMPO/O₂ system is composed from 3 steps, starting from AIBN/O₂ system, then validating AIBN/cumene/O₂ one and finally adding the corresponding reaction of DMPO. This last reaction mechanism consists of 30 species and 57 reactions.

The numerical solution of the non-linear differential equations corresponding to the mechanisms included in separate subsets and their analysis was carried out by the computer code KINAL [5].

For reasons to be explained later, experiments were also performed on the AIBN-induced oxidation of cumene in the absence of DMPO. Details concerning materials and methods have been described as already referred to [4].

RESULTS AND DISCUSSION

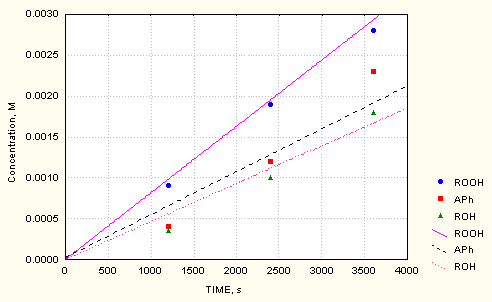
The reaction mechanism and the rate constants for the systems AIBN/O₂ are described in details in our earlier publication [6]. Rate constants for the AIBN/cumene/O₂ system were collected from literature sources (e.g. [7]). A critical review, however, revealed that in many cases these values show considerable differences depending on the various methods and experimental conditions applied at their determination. Therefore, the concentrations of cumyl hydroperoxide, cumylalcohol and acetophenon vs time up to 60 minutes have been additionally measured. Data together with the computed values are shown in Fig.1.

The fit between them and the measured ones is good. The following rate constants values have been used: k = 9.5 x10^-6 M^-1 s^-1 for the decomposition of AIBN [6]; k = 1.2 x10⁵ M^-1 s^-1 for the recombination of the RO₂ radicals [8]; k = 1x 10⁵ M^-1 s^-1 for the recombination of rO₂ [6]; k=0.47 M^-1 s^-1 for the chain propagation of the oxidation of cumene [9] and k = 5 M^-1 s^-1for the interaction of rO₂ with cumene [10].

During the course of processes in the systems AIBN/DMPO/O₂ and AIBN/cumene/DMPO/O₂ the following peroxy-type adducts can be formed:

DMPO + RO₂     Õ A1r          k=1.63e+2                                                                   (1)

DMPO + rO₂      Õ A3r           k=1.5e+3                                                                     (2)

DMPO + CH₃O₂ Õ A2r          k=1e+3                                                                        (3)

Where A1r, A2r and A3r are the corresponding adduct radicals.

Methylperoxy radicals are products of the b-scission of 1-cyano-1-propyloxyl radicals (rO) in the presence of oxygen, and formed in the combination process of rO₂ radicals.

Rate constants of reactions (1-2) are known from our previous measurements referred to in [4] while that of reaction (3) was defined by considering the reactivity of this radical in comparison with that of rO radicals.

Rate constants of mono- and bimolecular decomposition of A1r and A3r adducts have been determined already [4]:

A1r + A1r  Õ P           k=0.3                                                                                      (4)

A1r             Õ P           k=2.4e-4                                                                                 (5)

A3r + A3r   Õ P           k=0.3                                                                                      (6)

A3r             Õ P           k=2e-4                                                                                    (7)

Where P refers to any product. The corresponding values for the decomposition of A2r were assumed to be of similar magnitude:

A2r + A2r   Õ P          k=0.3                                                                                      (8)

A2r              Õ P          k=2.3e-4                                                                                 (9)

DMPO might react also with alkoxyl radicals. In this respect cumyloxyl (RO) and 1-cyano-1-propyloxyl (rO) radicals were considered as likely candidates:

rO + DMPO    Õ A4r              k=5e+6                                                                       (10)

A4r                  Õ P                  k=2e-4                                                                        (11)

A4r + A4r        Õ P                 k=0.3                                                                         (12)

RrO + DMPO  Õ A5r             k=5e+6                                                                       (13)

A5r                   Õ P                 k=2e-4                                                                       (14)

A5r + A4r Õ P                        k=0.3                                                                          (15)

With respect to their corresponding rate constants  the trapping of rO radicals is considerably faster than trapping of peroxyl radicals [11]

Measured rate constants for the radical induced decomposition of the adducts are not available yet. Therefore, the following values have been used:

A1r + RO₂      Õ P       k=2.0e+2                                                                               (16)

A1r + rO₂        Õ P      k=1.3e+4                                                                               (17)

A1r + CH₃O₂  Õ P      k=2.7e+4                                                                               (18)

A3r + RO₂      Õ P       k=2.0e+2                                                                               (19)

A3r + rO₂        Õ P      k=1.3e+4                                                                               (20)

A3r + CH₃O₂   Õ P      k=2.7e+4                                                                              (21)

A2r + RO₂          Õ P     k=2.0e+2                                                                              (22)

A2r + rO₂            Õ P     k=1.3e+4                                                                              (23)

A2r + CH₃O₂    Õ P     k=2.7e+4                                                                              (24)

A1r + rO          Õ P     k=1.0e+9                                                                               (25)

A3r + rO          Õ P     k=1.0e+9                                                                               (26)

A2r + rO          Õ P     k=1.0e+9                                                                               (27)

Finally, the cross-combination of the peroxyl adducts were also included:

A1r + A2r   Õ P          k=0.3                                                                                     (28)

A1r + A3r   Õ P          k=0.3                                                                                     (29)

A2r + A3r   Õ P          k=0.3                                                                                     (30)

Results are shown for two cases. Fig.2 displays the accumulation of A3r adduct in the AIBN/DMPO/O₂ system.

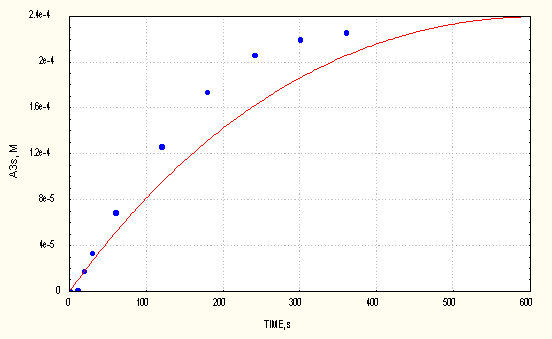Fig. 2 Measured and computed (full line) values of A3r adduct vs time in the AIBN/O₂/DMPO system ([DMPO]₀ = 1e-3 M)

Fig.3 shows the accumulation of A1r adduct in the AIBN/cumene/DMPO/O₂ system.

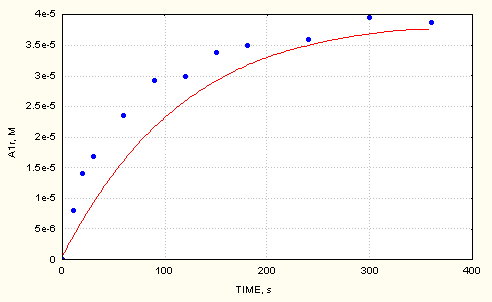Fig. 3 Measured and computed (full line) values of A1r adduct vs time in the AIBN/cumene/O₂/DMPO system ([DMPO]₀ = 2.9e-3 M)

As it can be seen, the agreement between the measured and computed maximum concentrations of the adducts is quite good. The time scale between measured and computed cases differs more. According to variance analysis, values especially of the bimolecular decompositions of the A1r and A3r adducts are mean values within limits of ± 0.2 [4].The effect of these reactions becomes more pronounced with increasing reaction time and can influence significantly the time to reach the maximum concentration values of the adducts. Taking this into consideration together with the complexity of the reaction mechanism, we consider the agreement to be informative in this respect, too.

The computed profiles of adduct accumulations clearly demonstrate linearity during the initial period, thus confirming that the decomposition of spin adducts can be neglected in that time period.

In spite of the fact that the radical induced reactions and cross combinations of alkoxyl radicals were not included into the reaction mechanism, the agreement between measured and computed results is satisfactory, it can be assumed that the role of alkoxyl adducts is minor.

Further analysis of the computed data by contribution and sensitivity methods can reveal more information on the main reaction channels and also on the most influential rate constants.

REFERENCES

[1] Gál, D. (1992) Biochem. Biophys. Res. Commun. 186: 1032-1036.

[2] Shulyakovskaya, T., Sümegi, L., and Gál, D.(1993) Biochem. Biophys. Res. Commun. 195: 581-587.

[3] Kriska, T., Maltseva, E., and Gál, D. (1993) Biochem. Biophys. Res. Commun. 223: 136-141.

[4] Shutova, T., Kriska, T., Németh, A., Agabekov, V., and Gál, D. (1999) Biochem. Biophys. Res. Commun. 270: 125-130.

[5] Turányi, T. (1990) Computers & Chemistry 14: 253-254.

[6] Vasvári, G., Kuramshin, E. M. Holly, S. Vidóczy, T., and Gál, D. (1988) J. Phys. Chem. 92: 3810-3818.

[7] Landolt-Börnstein, (1984) Numerical Data and Functional Relationships in Science and Technology, Radical Reaction Rates in Liquids (Hellwege, K. H., Madelung, O., and Fisher, H. Eds.) Vol. 13, Subvolume d, Springer-Verlag, Berlin

[8] Kaloerova, V. G., Nikolaevskii, A. N., Kucher, R.V., and Batrak, T.A. (1978) Dokl. Akad. Nauk SSSR 242:641.

[9] Beljakov, V. A., Kortenska, V., Rafikova, V., and Yanishlieva, N. (1991) Oxid. Commun. 14: 132.

[10] Schwetlick, K. (1988) J. Chem. Soc. Perkin Trans. 11: 2007-2010.

[11] Janzen, E. G., Krygsman, P. H., Lindsay, D. A., and Haire, D. L. (1990) J. Am. Chem. Soc. 112: 8279-8284.