3. TARGET THEORY

Much of the experimental work in radiation biology involves dose-response relationships. The fraction of damaged biological entities C*/C₀ may be plotted against the dose. The resultant curves may be linear, increase and then level off, or have a steeper sigmoidal shape after an initial delay period (Fig. 12). Alternatively, the logarithm of the fraction of undamaged entities may be plotted against the dose. This type of plot is referred to as a survival curve. Experimental survival curves for irradiation of E. coli are shown in Fig. 13. In this context, "damage" refers specifically to a measured endpoint. Undetected or sub-lethal damage may accumulate which eventually is expressed as an observable endpoint. Target theory is a

 Figure 12. Dose-response curves. (a) zero-order process, (b) first-order process, (c) second-order process, (d) four-hit process. (Adapted from Grossweiner.)

phenomenologicalapproach to biological radiation damage which provides insights into the damage mechanisms in terms of the survival curves. The basic assumption of target theory is that an observable response takes place when a localized region of a

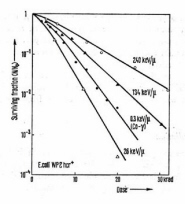
Figure 13. Survival curves for inactivation of E. coli by ⁶⁰Co gamma-rays and alpha-particles with different LET. The curvature at low dose levels is indicative of sub-lethal damage and/or repair. (Adapted from Dertinger and Jung.)

biological system or a target absorbs one or more units of energy referred to as hits. The hit concept implies that radiation damage is a discrete process. Every damaging event may not constitute a hit owing to the location of the lesion and the action of repair processes. Target theory assumes that radiation damage is a random process. The distribution of hits should follow a Poisson distribution, which applies for a large number of equivalent trials in which the probability of success on a single trial is very low. For example, the number of random typographical errors per chapter in a printed book obeys a Poisson distribution. If n_ave is the average number of errors per chapter in the entire book, the probability of finding exactly n errors in a given chapter is given by:

(6): p(n) = Exp(-n_ave) (n_ave)ⁿ / n!

Thus, if the average number of errors per chapter is 5, the probability that any one chapter has exactly one error is: 5 x Exp(-5)/1! = 0.0337 and the probability of exactly five errors is: 5⁵ x Exp(-5)/5! = 0.1755. The probability of finding one or more errors per chapter is 1 – p(0) which is 0.9933. An equivalent analysis applies for hits on biological targets, where n_ave is proportional to the radiation dose. The "one-hit model" assumes that a single hit on one target leads to the observed response. Since p(0) is the probability that no hits have occurred, the surviving fraction (F) of undamaged targets equals p(0):

(7): F = Exp(-n_ave)

For direct action n_ave can be expressed as:

(8): n_ave = Dr_Tv_T/W

where D is the dose (eV/g), v_T is the target volume (cm³), r_T is the target density (g/cm³), and W (eV) is the energy equivalent of a hit. The usual assumption in radiation biology is that W equals the average energy to form an ion-pair in water which is estimated as about 50-60 eV. It follows from Equation (7) that the surviving fraction equals 1/e = 0.37 when n_ave = 1. The corresponding absorbed dose is D₃₇ :

(9): 1/D₃₇ = v_T/W

Thus, 1/D₃₇ equals the radiation sensitivity (S) for the one-hit model and the graph of Log_e F vs D should be a straight line with the slope equal to S. The molecular weight of the target is given by:

(10): MW_T = 9.63 x 10⁷ W/D₃₇

where W is in eV and D is in Gy. For example, if 5 x 10⁴ Gy is required to inactivate 63% of a dry virus layer, the effective molecular weight of the target is 1.1 x 10⁵ dalton.

Many survival curves have an initial curved region followed by a steeper linear decrease at high dose. The initial stage is attributed to sub-lethal damage. This response can occur if more than one target must be damaged or if more than one hit on a single target is required to initiate the observed effect. Alternatively, the earlier damage may undergo repair by chemical or enzymic processes and converted to non-lethality. The one-hit model may be extended to the case where one hit is required on each of m equivalent targets to achieve an observable effect. The damaged fraction of targets equals [1 - Exp(-n_ave)] for one target and [1 - Exp(-n_ave)]^m for m targets where n_ave is given by Eq. (8). The surviving fraction is:

(11): F = 1 - [1 - Exp(-n_ave)]^m

Figure 14 shows semi-logarithmic plot of Equation (11) for different values of n. The low-dose shoulder corresponds to sub-lethal damage during the initial period while hits are accumulating. Expanding the right side of Equation (11) shows that in the limit of high dose: F @ mExp(-n_ave). The survival curve has a linear slope (1/D_o) in the high-dose regime. This line intercepts the vertical axis at the "extrapolation number" (m). The "threshold dose" (D_th) is defined as the initial dose at which the extrapolated high-dose line intercepts S = 1. Setting S = 1 gives: Log_e m = D_th/D_o. Examination of Fig. 14 shows that: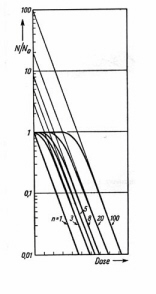

Figure 14. Theoretical survival curves for n hits on a single target. The extrapolation of the high dose line gives the hit number. (Apadpted from Zimmer.)

D₃₇ = D_o + D_th. D₃₇ is higher than in the single-hit model because all m targets must accumulate at least one hit before 63% of the systems respond. D_o is the equivalent of the one-hit D₃₇ as defined by Equation (5). More complicated models have been proposed for radiation inactivation of mammalian cells. The assumption that a cell has g equivalent sites, each of which is an r-target entity, and that damage to any site is lethal leads to:

(12): F = {1 - (1 - Exp[-(D/D_o)]^r}^g

The extrapolation number for this case is r^g. Multi-hit kinetics (n > 1) are required when a single target must acquire more than one hit to initiate a response. The plots of the damaged fraction C*/C₀ vs D are S-shaped (Fig. 12). However, the hit number can be calculated from the relative dose required to attain any two values of F. For example, if D₉₀ is the dose at 90% survival and D₅₀ is the dose at 50% survival, then the analysis shows that D₅₀/D₉₀ = 3.322 for n = 1, 2.320 for n = 2, 1.711 for n = 5, 1.472 for n = 10, 1.372 for n = 15, 1.253 for n = 30, etc. A more complicated case obtains when n hits are required on each of m equivalent targets. The modeling equations are usually not of practical value because different combinations of n and m can lead to survival curves of similar shape. An empirical survival curve of the type:

(13): F = Exp[-aD + bD²]

was proposed for mammalian cell damage in the theory of dual radiation action. Parameter-a measures the probability of "one-hit" damage and parameter-b measures the efficiency of "two-hit" damage. Experimental values of a/b for mammalian cells are much larger for fast neutrons than for x-rays. This result suggests that a single neutron hit is more lethal than a single photon hit. Although target theory is a useful model for characterizing biological radiation damage, this phenomenological theory does not lead to definitive information about the actual damage mechanisms.

3.1. Effect of LET on Radiation Sensitivity

Comparisons between D₃₇ for different types of radiation are quantified by the RBE. This dimensionless quantity is proportional to the inverse of the dose leading to a given biological effect under identical conditions for different types of radiation. RBE is usually scaled to gamma-rays. LET is an important determinant of RBE. The passage of high LET radiation (e.g., protons) through a target has a higher probability for generating an ion-pair within the target than low LET radiation (e.g., x-rays) owing to the denser ionization track. Thus, RBE should increase with increasing LET. However at very high LET, multiple ionisations may be wasted within the target and the RBE decreases. The track segment model of Howard-Flanders was an early theoretical approach to the effect of LET on radiation sensitivity. The analysis for the one-hit case (n = 1) shows that the radiation sensitivity S decreases from low to high LET because the extra hits generated by high LET radiation are wasted. However for n > 1, S increases to a peak value that depends on the hit number n and then falls off at higher LET. Radiation inactivation of enzymes, viruses, and haploid cells may follow a one-hit model, while diploid cells are expected to be act as two-hit targets.

4. INDIRECT ACTION OF IONIZING RADIATION

Indirect action in aqueous and biological systems involves the radiation chemistry of liquid water. The primary products of water radiolysis are generated with a non-uniform spatial distribution owing to the inhomogeneous distribution of the initial energy loss. The analysis of the early-time regime is based on spur theory. Those primary species that survive spur reactions eventually attain a random spatial distribution in the medium. The later-time regime obeys conventional homogeneous reaction kinetics. Homogeneous kinetics may not be applicable when a small intermediate, e.g., a free radical, reacts with a large biological target such as a macromolecule, cell organelle, or whole cell, because diffusional processes cannot maintain a uniform concentration of the reacting species. This situation has been modeled with large target reaction kinetics.

3.1. Homogeneous Reaction Kinetics

The kinetics of chemical reactions are described in terms of molecular order and reaction order. Molecular order refers to the actual number of species that take part in a chemical reaction. Virtually all chemical reactions in water take place between two reacting species, one of which may be a solvent molecule. For example, the reactive species in proton dissociation are an acidic molecule or ion and an adjacent water molecule. Reaction order refers to the dependence of the reaction rate on the actual concentration of the reactants. The rate of a zero-order reaction is constant in time, e.g., oxidation of glucose in the liver. The rate of a first-order reaction is proportional to the concentration of one reactant, e.g., dissociation of an enzyme-substrate complex. The rate of a second-order reaction is proportional to the product of two reactant concentrations or the square of one reactant concentration. Fast reactions of small free radicals in the liquid phase are usually of second-order. Third-order reactions occur in the gas phase because a "third body" is required to conserve energy and momentum. An inert gas or the wall of the containing vessel may serve as a third body. A bimolecular reaction may appear to be of first-order if one reacting species is present in large excess, e.g., proton dissociation. This type of process is referred to as "pseudo-first order". The proportionality constants in kinetics equations are referred to as rate constants, although their numerical values may depend on the temperature, pH, and ionic strength. The rate constant of a very fast reaction may vary in time during a short period after a species is generated because diffusion may not be able to keep up with depletion of the primary species. This effect is closely related to spur theory.

Conventional reaction kinetics express the reaction rate in the form of total differential equations which are then solved for the relevant concentrations. A uniform spatial distribution of the constituents is assumed, which rules out the application of this approach to spur reactions. A unimolecular process can be expressed as:

A v products

If the reaction rate does not depend on the amount of species-A the integrated rate equation is:

(14): [A] - [A]₀ = k₀t

where [A] is the molar concentration of A, [A]_o is its initial concentration, and k₀ (mole/liter-s) is the zero-order rate constant. A graph of [A] vs t is linear with the slope equal to - k₀. The reaction half time is 1/2k₀ which does not depend on [A]₀. The same reaction is of first-order if the instantaneous reaction rate is proportional to the unreacted concentration of species A. The corresponding rate equation is:

(15): Log₁₀ [A]/[A]₀ = - k₁t/2.303

where k₁ (s^-1) is the first-order rate constant. A plot of Log₁₀ [A] vs t is linear with the slope equal to - k₁/2.303. The reaction half-time equals 0.693/k₁ which is independent of the starting concentration. Radioactive decay exemplifies a first-order reaction. A second-order reaction can be represented as:

A + A v products

with the rate equation:

(16): [A] = [A]₀ / (1 + 2k₂t)

where k₂ (liter/mol-s) is the second-order rate constant. A plot of 1/[A] vs t is linear with the slope 2k₂ and the intercept equal to 1/[A]_o. The half- time 1/2k₂[A]_o decreases with [A]₀ because the instantaneous reaction rate depends on [A]². First-order and second-order reactions can be distinguished by measuring the dependence of the half-time on the initial concentration. A second-order reaction between two different species is expressed by:

A + B v products

The general solution is easily found for different starting amounts of A and B. A special case obtains if [B] >> [A]. The reaction is then of pseudo-first order and follows Equation (15) with k₁ replaced by k₂[B]. Figure 12 depicts the dose-response curves for zero-order, first-order, and second-order reactions.

3.2 Diffusion-Limited Rate Constants

Many bimolecular reactions of small free radicals are exothermic and generate energetic or "hot" products in the gas phase. When the reaction takes place in solution, the excess kinetic energy is carried away by nearby solvent molecules - this phenomenon is the cage effect. Owing to the rapid thermal equilibration of the products, the effective reaction rate is then controlled by diffusional encounters between the reactants. The following expression was derived by Debye for the bimolecular rate constant of a diffusion-limited reaction between two electrically charged species:

(17): k_AB = (4pN₀ a_AB R_AB/1000) (K/e^K - 1)

where R_AB (cm) is the sum of the radii of reacting species A and B, a_AB (cm²/s) is the sum of the reactant diffusion constants, and K / Z_AZ_Be²/4pe₀kk_BT, where Z_A and Z_B are the charges on species A and B, e is the electron charge, e₀ is the permittivity constant 8.85 x 10^-12, k is the relative dielectric constant of the medium, k_B is the Boltzmann constant, and T is the absolute temperature. [K in Equation (17) is expressed SI units. In cgs units 4pek is replaced by the relative dielectric constant of the medium.] K is zero if either A or B is uncharged. Approximate values of k_AB can be found by using the Stokes' law expression for the diffusion constant of a spherical particle:

(18): a = kT/3phD

where D is the diameter of the molecule and h is the viscosity of the medium. (The viscosity of water is 1 poise at 20.2EC; 10 poise = 1 J-s/m³). A typical calculation for bimolecular reactions of hydroxyl radicals in water gives k (OH+OH) = 2 x 10⁹ liters/mol-s which is in good agreement with experimental measurements.

Various techniques have been devised to measure the rate of fast chemical reactions. In pulse radiolysis a system is irradiated with an intense pulse of ionising radiation, typically < 1 ns in duration. A LINAC is a practical source of fast electrons and gamma-rays. Each radiation pulse generates a non-equilibrium concentration of the short-lived intermediates which can be identified and followed in real time by making fast optical absorption measurements. A typical experimental arrangement is depicted in Fig.15. In kinetic spectrophotometry the optical transmission of the irradiation cell is monitored continuously at selected wavelengths. This technique makes it possible to follow the disappearance of a parent substance and the buildup and decay of intermediate products. In an alternative pulse-probe technique the entire absorption spectrum of the irradiated system is measured at a selected short time delay after the irradiation pulse using a broad-spectrum light flash as the spectral source.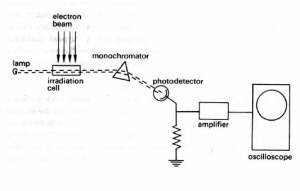

 Figure 15. Schematic of pulse radiolysis apparatus for kinetic spectrophotometry. This system follows the optical absorption of the sample at single wavelengths before, during, and after a pulse of ionising radiation. The spectra of short-lived reaction products are analyzed by plotting the optical signals at different wavelengths and fixed time delays after the irradiation pulse. (Adapted from Swallow.)

Pulse radiolysis studies have led to the identification of many short-lived intermediates and measurements of reaction rate constants. The competition method is a continuous irradiation technique in which the dependence of a product yield on the concentration of an added solute leads to relative rate constants. The competition method is used also in conjunction with pulse irradiation methods, in which case the effect of an additive on the decay of a transient product is measured in real time.

3.3. Steady-State Competition Kinetics

Steady-state reaction kinetics are based on the assumption that the short-lived intermediates are present in very low concentrations under continuous irradiation. Consider the indirect action of ionising radiation on biological entities (T) irradiated in the presence of an additive (A) which competes for the short-lived radical intermediates (R). The relevant reactions are:

H₂O Y R + other species

R + A v products (k_s)

R + T vT’ (k_T)

where Y denotes a primary radiolysis reaction, k_s and k_T are bimolecular rate constants, and T’ is the damaged target. A straightforward kinetics analysis leads to the dependence of 1/D₃₇ on the target and additive concentrations:

(19): 1/D₃₇ = bG_R /{[T]₀ + (k_A/k_T) [A]}

where G_R is the G-value for production of the primary radicals, k_A is the bimolecular rate constant for primary radical reactions with the additive, [T]₀ is the initial concentration of targets, and b = 1.038 x 10^-7 is a numerical factor for D₃₇ in Gy. For a constant target concentration, Eq. (19) leads to the dependence of D₃₇ on the additive concentration and, therefore, the ratio k_A/k_T. D₃₇ can be measured for any property of the target that is affected by the primary radicals. The competition method is useful for relative measurements of different free radicals with biological targets.

3.4. Large Target Reaction Kinetics

Conventional bimolecular reaction kinetics are inaccurate for reactions of small entities with widely-separated large targets owing to depletion of the reactive entity near the surface of a large target faster than can be replenished by diffusion. This section was written by the author to exemplify a practical theoretical approach. The reaction volume (V ) around each large target is the volume of medium in which a radical has a 63% chance of diffusing to the target surface in competition with its reactions with a homogeneously distributed scavenger. The reaction volume is related to the average number of "hits" on the target surface according to:

(20): n_ave = Q Vc

where Q is the average number of small entities per unit volume of medium and c is the probability that the entity which reaches the surface of the large target initiates a "hit". The application of Eq. (20) to indirect action of small free radicals leads to:

(21): n_ave = 6.25 x 10⁹ DrS G_RV_Rc_R

where D (Gy) is the dose, V_R (cm³) is the reaction volume for indirect action of radicals R, and r (g/cm³) is the density of the medium. The summation includes all types of radicals that react with the target. The exact calculation of V_R for a spherical target of radius R_T based on diffusion theory gives:

(22): V_R (sphere) = 4pR_Td_R²(1 + R_T/d_R)

where d_R is the average diffusion distance of the radicals, which depends on the properties of the radicals, the medium, and the presence of scavengers which react with the radicals. The same result is obtained less rigorously by taking V_R as the volume of medium concentric with the sphere from r = R_T to r = (R_T + d_R) and dropping the d_r³ term. A similar approximate calculation for a long cylindrical target leads to:

(23): V_R (cylinder) = pL_Td_R² (1 + R'_T/d_R)

where L_T is the stretched-out length of the target and R'_T is the cylinder radius. The diffusion length depends on the pseudo-first order reactions of radicals with scavengers according to:

(24): d_R = /(a_R/S k_RjC_j)

where k_Rj is the bimolecular rate constant for reactions of radicals of type R with solute j, C_j is the concentration of scavengers of type j, and a_R is the diffusion constant of radicals of type R. Thus, the number of hits by one type of radical with a large spherical target is given by:

(25): n_ave = 4p x 6.25 x 10⁹ DG_Rc_R R_Td_R²(1 + R_T/d_R)

For a one-hit case D₃₇ is attained at n_ave = 1 leading to:

(26): S = 1/D₃₇ = 4p x 6.25 x 10⁹ G_Rc_R R_Td_R²(1 + R_T/d_R)

Equation (26) gives the radiation sensitivity for reactions of a reactive radical with a large spherical target. In the limit of a long-lived radical compared to the diffusion length (d_R >> R_T):

(27): S = 1/D₃₇ . 6.25 x 10⁹ G_R c_R (4pR_Ta_R)/ S k_RjC_j

The term in (..) is the same as diffusion-limited rate constant for bimolecular reactions of an uncharged radical; see Equation (17). Equation (27) is the same result as calculated by homogeneous reaction kinetics in which reactions of radicals with targets compete with scavenging. In the other limit of a very large target (R_T >> d_R). Equation (26) shows that 1/D₃₇ depends on R_T²d_R. This is result differs from the results of homogeneous reaction kinetics which lead to a linear dependence of S on R_T. The reactions of the primary water radiolysis radicals generated in the cytoplasm with chromosomal DNA are an important application. The same analysis can be used for reactions of short-lived photochemical species with large targets such as singlet molecular oxygen, in which case d_R = /2at where t is the singlet oxygen decay lifetime.

Next section

RADIATION CHEMISTRY OF WATER